
如图,顺次连接边长为1的正方形ABCD四边的中点,得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点,得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点,得到四边形A3B3C3D3,…,按此方法得到的四边形A8B8C8D8的周长为 .
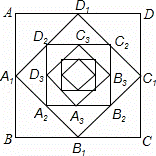
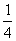
【解析】顺次连接正方形ABCD四边的中点得正方形A1B1C1D1,则得正方形A1B1C1D1的面积为正方形ABCD面积的一半,即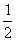 ,则周长是原来的
,则周长是原来的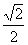 ;
;
顺次连接正方形A1B1C1D1中点得正方形A2B2C2D2,则正方形A2B2C2D2的面积为正方形A1B1C1D1面积的一半,即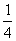 ,则周长是原来的
,则周长是原来的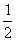 ;
;
顺次连接正方形A2B2C2D2得正方形A3B3C3D3,则正方形A3B3C3D3的面积为正方形A2B2C2D2面积的一半,即 ,则周长是原来的
,则周长是原来的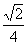 ;
;
顺次连接正方形A3B3C3D3中点得正方形A4B4C4D4,则正方形A4B4C4D4的面积为正方形A3B3C3D3面积的一半 ,则周长是原来的
,则周长是原来的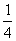 ;
;
…
故第n个正方形周长是原来的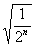 ,
,
以此类推:正方形A8B8C8D8周长是原来的 ,
,
∵正方形ABCD的边长为1,
∴周长为4,
∴ 按此方法得到的四边形A8B8C8D8的周长为
按此方法得到的四边形A8B8C8D8的周长为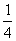 .
.


科目:初中数学 来源: 题型:
如图是二次函数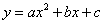 图象的一部分,图象过点
图象的一部分,图象过点 (-3,0),对称轴为直线
(-3,0),对称轴为直线 ,给出四个结论:
,给出四个结论:
①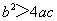 ; ②
; ②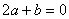 ; ③
; ③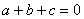 ; ④
; ④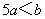 .
.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
海南有丰富的旅游产品.某校九年级(1)班的同学就部分旅游产品的喜爱情况对游客随机调查,要求游客在列举的旅游产品中选出喜爱的产品,且只能选一项,以下是同学们整理的不完整的统计图:
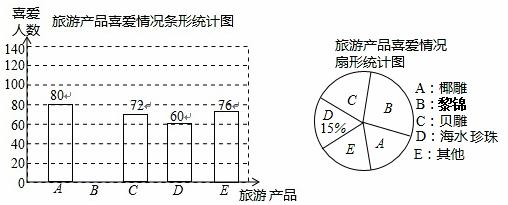
根据以上信息完成下列问题:
(1)请将条形统计图补充完整;
(2)随机调查的游客有 人;在扇形统计图中,A部分所占的圆心角是 度;
(3)请根据调查结果估计在1500名游客中喜爱黎锦的约有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是池塘两端,设计一方法测量AB的距离,取点C,连接AC、BC,再取它们的中点D、E,测得DE=15米,则AB=( )米.
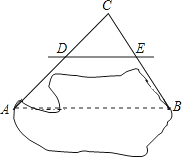
A.7.5 B.15 C.22.5 D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
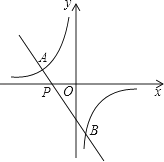
如图,一次函数y=kx+b(k≠0)的图象过点P(﹣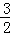 ,0),且与反比例函数y=
,0),且与反比例函数y=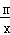 (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
查看答案和解析>>
科目:初中数学 来源: 题型:
小宋作出了边长为2的第一个正方形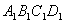 ,算出了它的面积.然后分别取正方形
,算出了它的面积.然后分别取正方形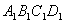 四边的中点
四边的中点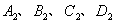 作出了第二个正方形
作出了第二个正方形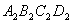 ,算出了它的面积.用同样的方法,作出了
,算出了它的面积.用同样的方法,作出了
第三个正方形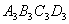 ,算出了它的面积 ,由此可得,第六个正方形
,算出了它的面积 ,由此可得,第六个正方形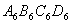 的面积
的面积
是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2.
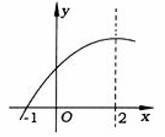
下列结论:
①4a+b=0;
②9a+c>3 b;
b;
③8a+7b+2c>0;
④当x>-1时,y的值随x值的增大而增大.
其中正确的结论有( )
A. 1个 B.2个 C.3个 D.4个
1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
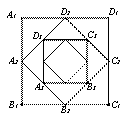
把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
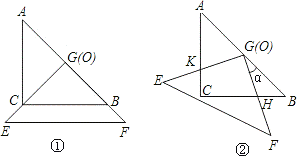
(1)在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论;(要有辅助线哟!)
(2)连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的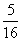 ,若存在,求出此时x值;若不存在,说明理由.
,若存在,求出此时x值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com