
把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
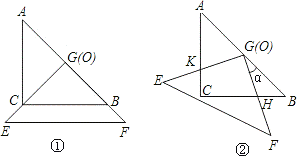
(1)在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论;(要有辅助线哟!)
(2)连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的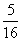 ,若存在,求出此时x值;若不存在,说明理由.
,若存在,求出此时x值;若不存在,说明理由.
(1)BH=CK,四边形CHGK的面积不变;
(2)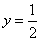 x2-2x+4, 0<x<4;
x2-2x+4, 0<x<4;
(3)当x=1或x=3时,△GHK的面积均等于△ABC的面积的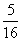
【解析】(1)在上述旋转过程中,BH=CK,四边形CHGK的面积不变
连接CG,
∵△ABC为等腰直角三角形,O(G)为其斜边中点,∴CG=BG,CG⊥AB,∴∠ACG=∠B=45°,∵∠BGH与∠CGK均为旋转角,∴∠BGH=∠CGK,在△BGH与△CGK中,∠B=∠KCG,BG=CG, ∠BCG=∠CGK∴△BGH≌△CGK(ASA),∴BH=CK,S△BGH=S△CGK.∴S四边形CHGK=S△CHG+S△CGK=S△CHG+S△BGH=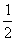 S△ABC=
S△ABC=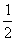 ×
×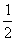 ×4×4=4即:S四边形CHGK的面积为4,是一个定值,在旋转过程中没有变化;
×4×4=4即:S四边形CHGK的面积为4,是一个定值,在旋转过程中没有变化;

(2)∵AC=BC=4,Bk=x,∴CH=4-x,CK=x,连 接HK.
接HK.
由S△GHK=S四边形CHGK-S△CHK,得y=4-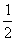 x(4-x)=
x(4-x)=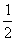 x2-2x+4 由0°<α<90°,
x2-2x+4 由0°<α<90°,
得到BH最大=BC=4,∴0<x<4;
(3)存在.根据题意,得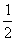 x2-2x+4=
x2-2x+4=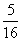 ×8
×8
解这个方程,得x1=1,x2=3,
即:当x=1或x=3时,△GHK的面积均等于△ABC的面积的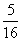 .
.


科目:初中数学 来源: 题型:
2、点A、B位于直线l的同侧,A、B关于直线l的对称点分别为点A'、B',点P在直线l上。当PA+PB最短时 点P是() a) AA'与l的交点 b)BB'与l的交点 c)BA'与l的交点 d)AB的延长线与l的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
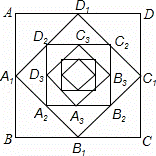
如图,顺次连接边长为1的正方形ABCD四边的中点,得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点,得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点,得到四边形A3B3C3D3,…,按此方法得到的四边形A8B8C8D8的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
某五金店购进一批数量足够多的p型节能电灯 进价为35元/只,以50元/只销售,每天销售20只.市场调研发现:若每只每降l元,则每天销售数量比原来多3只.现商店决定对Q型节能电灯进行降价促销活动,每只降价x元(x为正整数).在促销期间,商店要想每天获得最大销售利润,每只应降价多少元?每天最大销售毛利润为多少?(注:每只节能灯的销售毛利润指每只节能灯的销售价与进货价的差)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com