
 如图,Rt△ABC的内切圆⊙O与斜边AB切于点D,与两直角分别切于点E、S,DE与AC的延长线交于点F,请判断BD与CF有何关系?写出你的猜想,并加以证明.
如图,Rt△ABC的内切圆⊙O与斜边AB切于点D,与两直角分别切于点E、S,DE与AC的延长线交于点F,请判断BD与CF有何关系?写出你的猜想,并加以证明.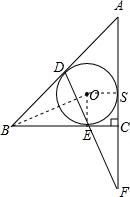 解:BD=CF.
解:BD=CF.
|


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
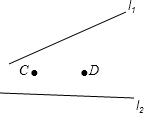 如图,一个人从C点骑马出发到D点,但他必须先到河岸边l1的P1点去让马饮水,然后再到河岸边l2的P2点去,再次让马饮水,最后骑马到D点,他应如何选择饮水点P1,P2.才能使所走的路程CP1+P1P2+P2D最短?
如图,一个人从C点骑马出发到D点,但他必须先到河岸边l1的P1点去让马饮水,然后再到河岸边l2的P2点去,再次让马饮水,最后骑马到D点,他应如何选择饮水点P1,P2.才能使所走的路程CP1+P1P2+P2D最短?查看答案和解析>>
科目:初中数学 来源: 题型:
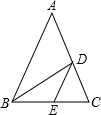 如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是
如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com