
【题目】综合与探究:如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在点
在点![]() 的左侧,与
的左侧,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的一个动点.
下方抛物线上的一个动点.
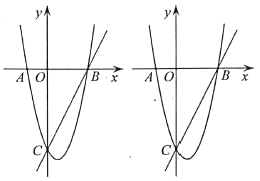
(1)求直线![]() 的解析式;
的解析式;
(2)连接![]() ,
,![]() ,并将
,并将![]() 沿
沿![]() 轴对折,得到四边形
轴对折,得到四边形![]() .是否存在点
.是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,求出此时点
为菱形?若存在,求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出此时点
的面积最大?求出此时点![]() 的坐标和四边形
的坐标和四边形![]() 的最大面积.
的最大面积.
【答案】(1)![]() (2)存在点
(2)存在点![]() 使四边形
使四边形![]() 为菱形,点
为菱形,点![]() 的坐标为
的坐标为![]() (3)当点
(3)当点![]() 运动到
运动到![]() 时,四边形
时,四边形![]() 的面积最大,四边形
的面积最大,四边形![]() 的最大面积为32
的最大面积为32
【解析】
(1)求出B、C的坐标,然后根据待定系数法即可求出一次函数的解析式;
(2)连接PP'交CO于点D.由菱形的性质得到,PC=PO,且PD⊥CO,OD=DC=4,即得到点P的纵坐标,代入二次函数解析式即可得到结论;
(3)如图2,连接PO,作PM⊥x轴于M,PN⊥y轴于N.设点P坐标为(m,m2-2m-8),根据![]() 求出四边形ABPC面积的表达式,然后根据二次函数的性质求解即可.
求出四边形ABPC面积的表达式,然后根据二次函数的性质求解即可.
(1)当![]() 时,
时,![]() .
.
解得![]() ,
,![]() .
.
∵点![]() 在点
在点![]() 的左侧,
的左侧,
∴点![]() ,
,![]() 的坐标分别是
的坐标分别是![]() ,
,![]() .
.
当![]() 时,
时,![]() .
.
∴点![]() 的坐标是
的坐标是![]() .
.
设直线![]() 的解析式为
的解析式为![]() .
.
将![]() ,
,![]() 两点的坐标代入
两点的坐标代入![]() ,
,
得![]() ,
,
解方程,得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(2)抛物线上存在点![]() ,使四边形
,使四边形![]() 为菱形.
为菱形.
如图1,连接![]() 交
交![]() 于点
于点![]() .
.
∵四边形![]() 为菱形,
为菱形,
∴![]() ,且
,且![]() ,
,![]() ,即点
,即点![]() 的纵坐标为-4.
的纵坐标为-4.
由![]() ,得
,得
![]() ,
,![]() (不合题意,舍去).
(不合题意,舍去).
所以存在点![]() 使四边形
使四边形![]() 为菱形,点
为菱形,点![]() 的坐标为
的坐标为![]() .
.

(3)如图2,连接![]() ,作
,作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() .
.
设点![]() 坐标为
坐标为![]() ,
,
∵点![]() 的坐标为
的坐标为![]() .
.
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]()
![]()
![]()
![]()
![]()
∴当![]() 时,
时,![]() .
.
此时点![]() 坐标为
坐标为![]() .
.
∴当点![]() 运动到
运动到![]() 时,四边形
时,四边形![]() 的面积最大,四边形
的面积最大,四边形![]() 的最大面积为32.
的最大面积为32.


科目:初中数学 来源: 题型:
【题目】某校七年级(1)班班主任对本班学生进行了“我最喜欢的课外活动”的调查,并将调查结果分为书法和绘画类记为A;音乐类记为B;球类记为C;其他类记为D.根据调查结果发现该班每个学生都进行了等级且只登记了一种自己最喜欢的课外活动.班主任根据调查情况把学生都进行了归类,并制作了如下两幅统计图,请你结合图中所给信息解答下列问题:
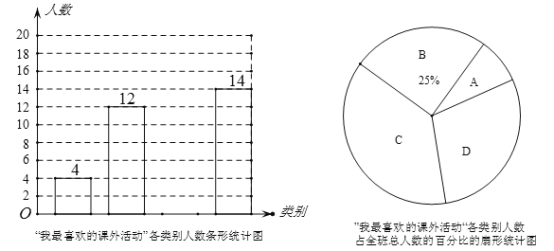
(1)七年级(1)班学生总人数为_______人,扇形统计图中D类所对应扇形的圆心角为_____度,请补全条形统计图;
(2)学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“迎元且大酬宾!”某商场设计的促销活动如下:在一个不透明的箱子里放有![]() 个相同的小球,球上分别标有“
个相同的小球,球上分别标有“![]() 元”、“
元”、“![]() 元”、“
元”、“![]() 元”和“
元”和“![]() 元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券.某顾客刚好消费
元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券.某顾客刚好消费![]() 元,
元,
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象的交点为
的图象的交点为![]() ,
,![]() 轴垂足为
轴垂足为![]() ,若点
,若点![]() 在反比例函数图象上,且
在反比例函数图象上,且![]() 的面积等于12,则点
的面积等于12,则点![]() 的坐标为__________.
的坐标为__________.
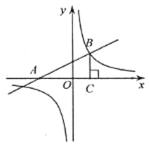
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蛋糕房推出一种新品蛋糕,每个成本为50元经过一段时间的售卖发现,当单价定为90元的时候,可卖100个,而单价每降低1元,就会多卖出10个
(1)写出销售量![]() (个)与销售单价
(个)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)若设销售这种蛋糕的利润为![]() (元),请写出
(元),请写出![]() 与销售单价
与销售单价![]() (元)之间的函数关系式,并计算当销售单价定为多少元时该蛋糕房可获得最大利润(不需要计算最大利润);
(元)之间的函数关系式,并计算当销售单价定为多少元时该蛋糕房可获得最大利润(不需要计算最大利润);
(3)若想尽可能地降低成本,并使该蛋糕房获利6000元,应将销售单价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
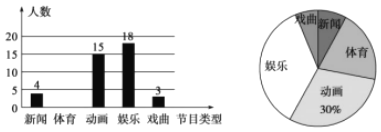
请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD边AD上的一个动点,且与点A、点D不重合,连结BE、CE,过点B作BF∥CE,过点C作CF∥BE,交点为F点,连接AF、DF分别交BC于点G、H,则下列结论错误的是( )
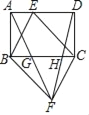
A. GH=![]() BC B. S△BGF+S△CHF=
BC B. S△BGF+S△CHF=![]() S△BCF
S△BCF
C. S四边形BFCE=ABAD D. 当点E为AD中点时,四边形BECF为菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com