
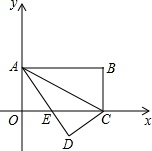
 вдЕуAЃЈ0ЃЌ2ЃЉЃЌBЃЈ4ЃЌ2ЃЉЃЌCЃЈ0ЃЌ4ЃЉЮЊЖЅЕуЕФЫФБпаЮOABCдкЦНУцжБНЧзјБъЯЕжаЮЛжУШчЭМЃЌЯжНЋЫФБпаЮOABCбижБЯпACелЕўЪЙЕуBТфдкЕуDДІЃЌADНЛOCгкEЃЎ
вдЕуAЃЈ0ЃЌ2ЃЉЃЌBЃЈ4ЃЌ2ЃЉЃЌCЃЈ0ЃЌ4ЃЉЮЊЖЅЕуЕФЫФБпаЮOABCдкЦНУцжБНЧзјБъЯЕжаЮЛжУШчЭМЃЌЯжНЋЫФБпаЮOABCбижБЯпACелЕўЪЙЕуBТфдкЕуDДІЃЌADНЛOCгкEЃЎЗжЮі ЃЈ1ЃЉЯШИљОнAASЖЈРэЕУГіЁїAEOЁеЁїCEDЃЌдйИљОнЙДЙЩЖЈРэЧѓГіOEЕФГЄЃЌНјЖјЕУГіEЕузјБъЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпAEЕФНтЮіЪНМДПЩЃЛ
ЃЈ2ЃЉЙ§DзїDGЁЭOCгкGЃЌПЩЕУГіЁїCDEЁзЁїDGEЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЧѓГіCDСНЕуЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпЕФНтЮіЪНМДПЩЃЛ
ЃЈ3ЃЉЂйЯШЧѓГіжБЯпACЕФНтЮіЪНЮЊЃЌЩшжБЯпPEНЛACгкHЃЌHЃЈmЃЌ-$\frac{1}{2}$m+4ЃЉЃЌЙ§HзїHMЁЭOAДЙзуЮЊMЃЌдђЁїAMHЁзЁїAOCЃЌИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЧѓГіHMЕФГЄЃЌНјЖјПЩЕУГіНсТлЃЛ
ЂкЗжEPЁЭABгыPEЁЭAEСНжжЧщПіНјааЬжТлМДПЩЃЎ
НтД№ 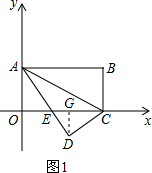 НтЃКЃЈ1ЃЉЁпЫФБпаЮOABCЮЊОиаЮЃЌЁїADCЪЧгЩЁїABCбиACЗелЖјГЩЃЌ
НтЃКЃЈ1ЃЉЁпЫФБпаЮOABCЮЊОиаЮЃЌЁїADCЪЧгЩЁїABCбиACЗелЖјГЩЃЌ
ЧвAЃЈ0ЃЌ2ЃЉЃЌBЃЈ4ЃЌ2ЃЉЃЌCЃЈ4ЃЌ0ЃЉЃЌдђDC=BC=OA=2ЃЌ
ЁЯD=ЁЯAOE=90ЁуЃЌЁЯAEO=ЁЯCEDЃЌ
дкЁїAEOгыЁїCEDжаЃЌ
$\left\{\begin{array}{l}{OA=CD}\\{ЁЯAOE=ЁЯCDE}\\{ЁЯAEO=ЁЯCED}\end{array}\right.$ЃЌ
ЁрЁїAEOЁеЁїCEDЃЈAASЃЉЃЌ
ЁрDE=OEЃЌ
ЩшOE=xЃЌдђEC=4-xЃЌ
ЁрЃЈ4-xЃЉ2=x2+22ЃЎ
ЁрOE=$\frac{3}{2}$ЃЌ
ЁрEЕуЮЊЃЈ$\frac{3}{2}$ЃЌ0ЃЉ
ЩшЙ§AЃЌEСНЕужБЯпНтЮіЪНЮЊy=kx+bЃЈkЁй0ЃЉЃЌдђ$\left\{\begin{array}{l}{\frac{3}{2}k+b=0}\\{b=2}\end{array}\right.$ЃЌ
ЁржБЯпAEЕФНтЮіЪНЮЊЃКy=-$\frac{3}{4}$x+2ЃЛ
ЃЈ2ЃЉЙ§DзїDGЁЭOCгкGЃЌЙЪЁїCDEЁзЁїDGEЃЌ
ЁпOE=$\frac{3}{2}$ЃЌ
ЁрEC=$\frac{5}{2}$ЃЌ
Ёр$\frac{DE}{EC}$=$\frac{DG}{CD}$ЃЌ$\frac{DE}{EC}$=$\frac{EG}{DE}$ЃЌМДDE=$\frac{3}{2}$ЃЌEG=$\frac{9}{10}$ЃЌ
ЁрDЃЈ$\frac{12}{5}$ЃЌ-$\frac{6}{5}$ЃЉЃЌ
гЩгкЙ§ЕуOЁЂDЁЂCЕФХзЮяЯпОЙ§дЕуЃЌдђЩшy=ax2+bxЃЌЖјCЃЈ4ЃЌ0ЃЉЃЌDЃЈ$\frac{12}{5}$ЃЌ-$\frac{3}{2}$ЃЉЃЌ
Ёр$\left\{\begin{array}{l}{16a+4b=0}\\{\frac{144}{25}a+\frac{12}{5}b=-\frac{3}{2}}\end{array}\right.$ЃЌНтЕУ$\left\{\begin{array}{l}{a=\frac{25}{64}}\\{b=-\frac{25}{16}}\end{array}\right.$ЃЌ
Ёрy=$\frac{25}{64}$x2-$\frac{25}{16}$xЃЌ
ЙЪОЕуFЕФзјБъЮЊFЃЈ4ЃЌ-$\frac{25}{16}$ЃЉЃЛ
3ЃЉЂйвзЧѓжБЯпACЕФНтЮіЪНЮЊyAC=-$\frac{1}{2}$x+2ЃЌЩшжБЯпPEНЛACгкHЃЌHЃЈmЃЌ-$\frac{1}{2}$m+2ЃЉЃЌ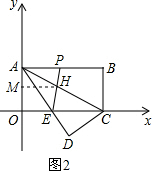
Й§HзїHMЁЭOAДЙзуЮЊMЃЌдђЁїAMHЁзЁїAOCЃЌ
Ёр$\frac{MH}{OC}$=$\frac{AH}{AC}$ЃЌ
ЁрSЁїEAHЃКSЁїFHC=1ЃК3Лђ3ЃК1ЃЌ
Ёр$\frac{AH}{AC}$=1ЃК3Лђ3ЃК1МД$\frac{AH}{AC}$=$\frac{MH}{OC}$=1ЃК4Лђ3ЃК4
ЁрHM=2Лђ3ЃЌЖјm=2Лђ3ЃЌ
ЁрH1ЃЈ2ЃЌ3ЃЉЃЌH2ЃЈ3ЃЌ1ЃЉЃЌ
ЁржБЯпEH1ЕФНтЮіЪНЮЊy=-$\frac{11}{4}$x+$\frac{17}{2}$ЃЌЕБy=4ЪБЃЌx=$\frac{18}{11}$
жБЯпEH2ЕФНтЮіЪНЮЊy=$\frac{7}{4}$x-$\frac{19}{2}$ЃЌЕБy=4ЪБЃЌx=$\frac{54}{7}$
ЙЪЕБt=$\frac{18}{11}$УыЛђ$\frac{54}{7}$УыЃЌжБЯпEPАбЁїEACЗжГЩУцЛ§жЎБШЮЊ1ЃК3СНВПЗжЃЎ
ЂкЕБEPЁЭABЪБЃЌ
ЁпAЃЈ0ЃЌ2ЃЉЃЌEЃЈ$\frac{3}{2}$ЃЌ0ЃЉ
ЕБPEЁЭAEЪБЃЌ
ЁпжБЯпAEЕФНтЮіЪНЮЊЃКy=-$\frac{3}{4}$x+2ЃЛ
ЩшжБЯпPEЕФНтЮіЪНЮЊy=$\frac{4}{3}$x+bЃЌ
ЁпEЃЈ$\frac{3}{2}$ЃЌ0ЃЉЃЌ
Ёр$\frac{4}{3}$ЁС$\frac{3}{2}$+b=0ЃЌНтЕУb=-2ЃЌ
ЁржБЯпPEЕФНтЮіЪНЮЊy=$\frac{4}{3}$x-2ЃЌ
ЁрЕБy=2ЪБЃЌx=3ЃЌ
ЁрAP=3ЃЌМДt=3ЃЈsЃЉЃЎ
злЩЯЫљЪіЃЌЕБt=$\frac{18}{11}$УыЛђ$\frac{54}{7}$УыЛђt=3УыЪБЃЌжБЯпEPАбЁїEACЗжГЩУцЛ§жЎБШЮЊ1ЃК3СНВПЗжЃЎ
ЕуЦР БОЬтПМВщЕФЪЧвЛДЮКЏЪ§злКЯЬтЃЌЩцМАЕНРћгУД§ЖЈЯЕЪ§ЗЈЧѓвЛДЮКЏЪ§МАЖўДЮКЏЪ§ЕФНтЮіЪНЁЂШЋЕШШ§НЧаЮМАЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪЃЌФбЖШНЯДѓЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | -Іа | BЃЎ | -3.1 | CЃЎ | -4 | DЃЎ | -2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
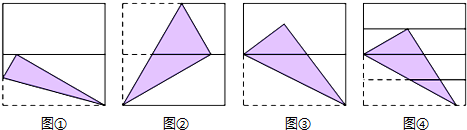
| AЃЎ | 4Иі | BЃЎ | 3Иі | CЃЎ | 2Иі | DЃЎ | 1Иі |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
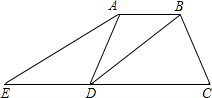 ШчЭМЃЌдкЬнаЮABCDжаЃЌABЁЮDCЃЌDBЦНЗжЁЯADCЃЌЙ§ЕуAзїAEЁЮBDЃЌНЛCDЕФбгГЄЯпгкЕуEЃЌЧвЁЯC=2ЁЯEЃЎ
ШчЭМЃЌдкЬнаЮABCDжаЃЌABЁЮDCЃЌDBЦНЗжЁЯADCЃЌЙ§ЕуAзїAEЁЮBDЃЌНЛCDЕФбгГЄЯпгкЕуEЃЌЧвЁЯC=2ЁЯEЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com