先化简.再求值:(2+$\frac{1}{a-1}$-$\frac{1}{a+1}$)÷.其中a=2．题目和参考答案——青夏教育精英家教网—

8．先化简，再求值：（2+$\frac{1}{a-1}$-$\frac{1}{a+1}$）÷（a-$\frac{a}{1-a}$），其中a=2．

分析原式括号中通分并利用同分母分式的加减法则计算，同时利用除法法则变形，约分得到最简结果，把a的值代入计算即可求出值．

解答解：原式=$\frac{2（a+1）（a-1）+a+1-a+1}{（a+1）（a-1）}$÷$\frac{a-{a}^{2}-a}{1-a}$=$\frac{2{a}^{2}}{（a+1）（a-1）}$•$\frac{a-1}{{a}^{2}}$=$\frac{2}{a+1}$，
当a=2时，原式=$\frac{2}{3}$．

点评此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案

一卷通AB卷快乐学习夺冠100分系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

18．

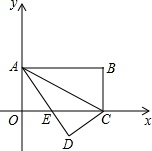以点A（0，2），B（4，2），C（0，4）为顶点的四边形OABC在平面直角坐标系中位置如图，现将四边形OABC沿直线AC折叠使点B落在点D处，AD交OC于E．
（1）试求E点坐标及直线AE的解析式；
（2）试求经过点O、D、C三点抛物线的解析式及顶点F的坐标；
（3）一动点P从点A出发，沿射线AB以每秒一个单位长度的速度匀速运动．
①当t为何值时，直线PE把△EAC分成面积之比为1：3的两部分；
②在P点的运动过程中，是否存在某一时刻使△APE为直角三角形？若存在，直接写出t的值；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．

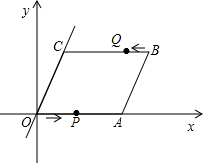如图，在直角坐标系中，点O是坐标原点，四边形OABC是平行四边形，点A的坐标为（14，0），点B的坐标为（18，4$\sqrt{3}$）
（1）写出点C的坐标（4，4$\sqrt{3}$）
（2）动点P从O出发，沿射线OA方向以每秒2个单位的速度运动，点Q从B出发以每秒1个单位的速度向点C运动，它们同时出发，当点Q到达点C时另一点也停止运动，设运动时间为t秒，求t为何值时，以P、Q、A、B为顶点的四边形是平行四边形．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

16．计算：（2$\sqrt{3}$+1）（$\sqrt{5}$+$\sqrt{6}$）=2$\sqrt{15}$+6$\sqrt{2}$+$\sqrt{5}$+$\sqrt{6}$．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

3．数据：6，5，4，2，8的平均数是5．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．设甲数为x，乙数为y，且甲数的$\frac{1}{3}$与乙数的和是甲、乙两数和的一半．
（1）求x，y满足的关系式；
（2）当x=6时，y是多少？当y=1时，x是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

20．计算：
（1）$\frac{2x-y}{x}-\frac{y}{y-2x}$；
（2）（-12x²y）²÷（-$\frac{3{x}^{2}}{y}$）²
（3）$\frac{2x-4}{{x}^{2}+3}÷\frac{x-2}{{x}^{2}+6x+9}$．