
【题目】观察下列两个数的积(这两个数的十位上的数相同,个位上的数的和等于![]() ),你发现结果有什么规律?
),你发现结果有什么规律?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
(1)设这两个数的十位数字为![]() ,个位数字分别为
,个位数字分别为![]() 和
和![]() ,请用含
,请用含![]() 和
和![]() 的等式表示你发现的规律;
的等式表示你发现的规律;
(2)请验证你所发现的规律;
(3)利用你发现的规律直接写出下列算式的答案.
![]() ;
; ![]() ;
; ![]() ;
;![]() .
.
【答案】(1)(10x+y)(10x+10-y)=100x(x+1)+y(10-y);(2)见解析;(3)3016;4221;5625;9025.
【解析】
(1)由题意得出每个数的积的规律是:十位数字乘以十位数字加一的积作为结果的千位和百位,两个个位数字相乘的积作为结果的十位和个位,据此可得出结果;
(2)利用整式的运算法则化简等式的左右两边,化简结果相等即可得出结论;
(3)根据(1)中的结论计算即可.
解:(1)由已知等式知,每两个数的积的规律是:十位数字乘以十位数字加一的积作为结果的千位和百位,两个个位数字相乘的积作为结果的十位和个位,
∴(10x+y)(10x+10-y)=100x(x+1)+y(10-y);
(2)∵等式左边=(10x+y)(10x+10-y)=(10x+y)[(10x-y)+10]=(10x+y)(10x-y)+10(10x+y)=100x2-y2+100x+10y;
等式右边=100x(x+1)+y(10-y)=100x2+100x+10y-y2=100x2-y2+100x+10y,
∴(10x+y)(10x+10-y)=100x(x+1)+y(10-y);
(3)根据(1)中的规律可知,
![]() 3016;
3016;![]() 4221;
4221;![]() 5625;
5625;![]() 9025.
9025.
故答案为:3016;4221;5625;9025.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.
(1)求证:△ABF∽△COE;
(2)当O为AC边中点, ![]() 时,如图2,求
时,如图2,求![]() 的值;
的值;
(3)当O为AC边中点, ![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
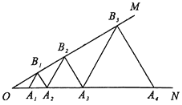
【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2,B3…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记a1,第2个等边三角形的边长记为a2,以此类推,若OA1=3,则a2=_______,a2019=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
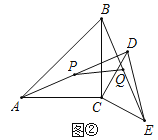
【题目】如图1,![]() ,
,![]() ,
,![]() ,AD、BE相交于点M,连接CM.
,AD、BE相交于点M,连接CM.![]() 求证:
求证:![]() ;
;![]() 求
求![]() 的度数
的度数![]() 用含
用含![]() 的式子表示
的式子表示![]() ;
;![]() 如图2,当
如图2,当![]() 时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断
时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断![]() 的形状,并加以证明.
的形状,并加以证明.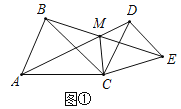
查看答案和解析>>
科目:初中数学 来源: 题型:
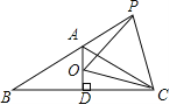
【题目】已知如图,等腰![]() 中,
中,![]() 于点
于点![]() ,点
,点![]() 是
是![]() 延长线上一点,点
延长线上一点,点![]() 是线段
是线段![]() 上一点,
上一点,![]() 下面的结论:①
下面的结论:①![]() ;②
;②![]() 是等边三角形;③
是等边三角形;③![]() ;④
;④![]() .其中正确的是( )
.其中正确的是( )
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里有若干个小球,它们除了颜色外,其它都相同,甲同学从袋子里随机摸出一个球,记下颜色后放回袋子里,摇匀后再次随机摸出一个球,记下颜色,…,甲同学反复大量实验后,根据白球出现的频率绘制了如图所示的统计图,则下列说法正确的是( )

A. 袋子一定有三个白球
B. 袋子中白球占小球总数的十分之三
C. 再摸三次球,一定有一次是白球
D. 再摸1000次,摸出白球的次数会接近330次
查看答案和解析>>
科目:初中数学 来源: 题型:
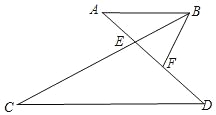
【题目】如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.
(1)求证:FB2=FEFA;
(2)若BF=3,EF=2,求△ABE与△BEF的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
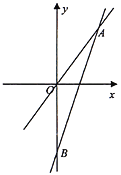
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与正比例函数
,与正比例函数![]() 的图象相交于点
的图象相交于点![]() ,且
,且![]() .
.
(1)分别求出这两个函数的解析式;
(2)求![]() 的面积;
的面积;
(3)点![]() 在
在![]() 轴上,且
轴上,且![]() 是等腰三角形,请直接写出点
是等腰三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com