
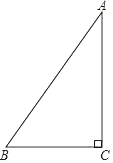
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)请用直尺和圆规作∠ABC的平分线,交AC于点D(保留作图痕迹,不要求写作法和证明);
(2)在(1)作出的图形中,若∠A=30°,BC=![]() ,则点D到AB的距离等于 .
,则点D到AB的距离等于 .
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
项目 选手 | 服装 | 普通话 | 主题 | 演讲技巧 |
李明 | 85 | 70 | 80 | 85 |
张华 | 90 | 75 | 75 | 80 |
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形ABC在平面直角坐标系中,直角边AC在x轴上,O为AC的中点,点A的坐标为(1,0),将△ABC绕点A顺时针旋转135°,使斜边AB的对应边A′B′与x轴重合,则点C的对应点C'的坐标为( )
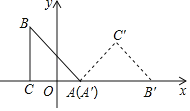
A. (2,2)B. (1+![]() ,
,![]() )C. (1+
)C. (1+![]() ,2)D. (2
,2)D. (2![]() ,2+
,2+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,ED切⊙O于点C,AD交⊙O于点F,连接AC,BF,且BF∥CD.
(1)求证:AC平分∠BAD;
(2)若⊙O的半径为![]() ,AF=2,求CD的长度.
,AF=2,求CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.

(1)求证:EG=CH;
(2)已知AF=![]() ,求AD和AB的长.
,求AD和AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,直径AB=10.sinA=![]() ,点D为线段AC上一动点(不运动至端点A、C),作DF⊥AB于F,连结BD,井延长BD交⊙O于点H,连结CF.
,点D为线段AC上一动点(不运动至端点A、C),作DF⊥AB于F,连结BD,井延长BD交⊙O于点H,连结CF.
(1)当DF经过圆心O时,求AD的长;
(2)求证:△ACF∽△ABD;
(3)求CFDH的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(8,0)、点B(0,4),点C、D分别是边OA、AB的中点.将△ACD绕点A顺时针方向旋转,得△AC′D′,记旋转角为α.

(I)如图①,连接BD′,当BD′∥OA时,求点D′的坐标;
(II)如图②,当α=60°时,求点C′的坐标;
(III)当点B,D′,C′共线时,求点C的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
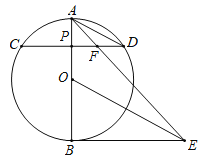
【题目】如图,AB为⊙O直径,P点为半径OA上异于O点和A点的一个点,过P点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE、DE、AE交CD于F点.
(1)求证:DE为⊙O切线;
(2)若⊙O的半径为3,sin∠ADP=![]() ,求AD;
,求AD;
(3)请猜想PF与FD的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com