
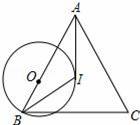
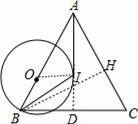
如图,在△ABC中,I是△ABC的内心,O是AB边上一点,⊙O经过B点且与AI相切于I点.若tan∠BAC=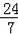
 ,则sin∠C的值为( )
,则sin∠C的值为( )

A.
 B.
B.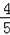
 C.
C.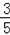
 D.
D.

B【考点】三角形的内切圆与内心.
【专题】计算题.
【分析】延长AI交BC于D,连结OI,作BH⊥AC于H,如图,根据内心的性质得∠OBI=∠DBI,则可证明OI∥BD,再根据切线的性质得OI⊥AI,则BD⊥AD,加上AI平分∠BAC,所以△ABC为等腰三角形,得到AB=AC,接着在Rt△ABH中,利用正切的定义得到tan∠BAH=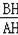
 =
=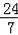
 ,于是可设BH=24x,AH=7x,利用勾股定理得到AB=25x,则AC=AB=25x,CH=AC﹣AH=18x,然后在Rt△BCH中,利用勾股定理计算出BC=30x,再利用正弦的定义计算sinC的值.
,于是可设BH=24x,AH=7x,利用勾股定理得到AB=25x,则AC=AB=25x,CH=AC﹣AH=18x,然后在Rt△BCH中,利用勾股定理计算出BC=30x,再利用正弦的定义计算sinC的值.
【解答】解:延长AI交BC于D,连结OI,作BH⊥AC于H,如图,
∵I是△ABC的内心,
∴BI平分∠ABC,即∠OBI=∠DBI,
∵OB=OI,
∴∠OBI=∠OIB,
∴∠DBI=∠OIB,
∴OI∥BD,
∵AI为⊙O的切线,
∴OI⊥AI,
∴BD⊥AD,
∵AI平分∠BAC,
∴△ABC为等腰三角形,
∴AB=AC,
在Rt△ABH中,tan∠BAH=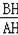
 =
=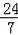
 ,
,
设BH=24x,AH=7x,
∴AB=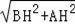
 =25x,
=25x,
∴AC=AB=25x,
∴CH=AC﹣AH=25x﹣7x=18x,
在Rt△BCH中,BC=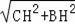
 =30x,
=30x,
∴sinC=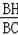
 =
=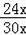
 =
=
 .
.
故选B.

【点评】本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了等腰三角形的判定与性质.


科目:初中数学 来源: 题型:
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
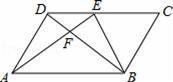

A.2:3 B.2:5 C.3:5 D.3:2
查看答案和解析>>
科目:初中数学 来源: 题型:
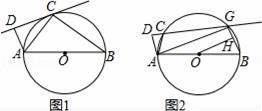
如图1,AB为⊙O的直径,C为⊙O上一点,作AD⊥CD,垂足为D.
(1)若直线CD与⊙O相切于点C,求证:△ADC∽△ACB;
(2)如果把直线CD向下平行移动,如图2,直线CD交⊙O于C、G两点,若题目中的其他条件不变,tan∠DAC=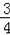
 ,AB=10,求圆心O到GB的距离OH的长.
,AB=10,求圆心O到GB的距离OH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
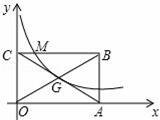
如图,矩形OABC的两点OA、OC分别在x轴、y轴的正半轴上,点G为矩形对角线的交点,经过点G的双曲线y=
 在第一象限的图象与BC相交于点M,交AB于N,若已知S△MBN=9,则k的值为 .
在第一象限的图象与BC相交于点M,交AB于N,若已知S△MBN=9,则k的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
华盛公司有甲、乙两个销售团队,同时销售同种产品,12个月后统计得出如下信息:甲销售团队第x个月销售量y1(万件)与x之间的函数关系为y1=a(x﹣4)2+
 ;乙销售团队第x个月销售量y2(万件)与x之间的函数关系为y2=kx+1(1≤x≤12,x为整数).甲、乙两个销售团队在第1个月的销售量相同,均为
;乙销售团队第x个月销售量y2(万件)与x之间的函数关系为y2=kx+1(1≤x≤12,x为整数).甲、乙两个销售团队在第1个月的销售量相同,均为
 (万件)
(万件)
(1)分别求y1、y2的函数解析式;
(2)探求有几个月乙销售团队比甲销售团队的销量高,并求当月最多高出多少万件?
(3)直接写出共有多少个月甲、乙两个销售团队的销售量均不低于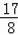
 万件.
万件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com