
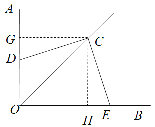
【题目】如图1,![]() ,
,![]() 平分
平分![]() ,以
,以![]() 为顶点作
为顶点作![]() ,交
,交![]() 于点
于点![]() ,
,![]() 于点E.
于点E.
(1)求证:![]() ;
;
(2)图1中,若![]() ,求
,求![]() 的长;
的长;
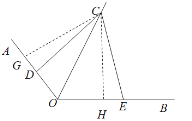
(3)如图2,![]() ,
,![]() 平分
平分![]() ,以
,以![]() 为顶点作
为顶点作![]() ,交
,交![]() 于点
于点![]() ,
,![]() 于点
于点![]() .若
.若![]() ,求四边形
,求四边形![]() 的面积.
的面积.

【答案】(1)见解析;(2)OD+OE =![]() ;(3)
;(3)![]()
【解析】
(1)过点C作CG⊥OA于G,CH⊥OB于H,然后根据题意利用AAS定理进行证明△CDG ≌ △CEH,从而求解;
(2)根据全等三角形的性质得到OD+OE =2OH,然后利用勾股定理求OH的值,从而求解;
(3)过点C作CG⊥OA于G,CH⊥OB于H,然后根据题意利用AAS定理进行证明△CDG ≌ △CEH,从而求得![]() =
=![]() =2
=2![]() ,然后利用含30°的直角三角形性质求得OH=
,然后利用含30°的直角三角形性质求得OH=![]() ,CH=
,CH=![]() 从而求得三角形面积,使问题得到解决.
从而求得三角形面积,使问题得到解决.
解:(1)如图,过点C作CG⊥OA于G,CH⊥OB于H,
∵![]() 平分
平分![]()
∴CG =CH
∵![]() ,
,![]()
∴∠CDO+∠CEO=180
∵∠CDG+∠CDO=180
∴∠CDG =∠CEO
在△CDG与△CEH中![]()
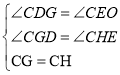
∴△CDG ≌ △CEH(AAS)
∴![]()
(2)由(1)得△CDG ≌ △CEH
∴DG=HE
由题易得△OCG与△OCH是全等的等腰直角三角形,且OG=OH
∴OD+OE=OD+OH+HE=OG+OH=2OH
设OH=CH=x,在Rt△OCH中,由勾股定理,得:
OH2+CH2=OC2
∴![]()
∴![]() (舍负)
(舍负)
∴OH =![]()
∴OD+OE =2OH=![]()
(3)如图,过点C作CG⊥OA于G,CH⊥OB于H,
∵![]() 平分
平分![]()
∴CG =CH
∵![]() ,
,![]()
∴∠CDO+∠CEO=180
∵∠CDG+∠CDO=180
∴∠CDG =∠CEO
在△CDG与△CEH中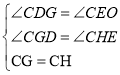
∴△CDG ≌ △CEH(AAS)
∴DG=HE
由题易得△OCG与△OCH是全等的直角三角形,且OG=OH
∴OD+OE=OD+OH+HE=OG+OH=2OH
∴![]() =
=![]() =2
=2![]()
在Rt△OCH中,有∠COH=60°,OC=3,
∴OH=![]() ,CH=
,CH=![]()
∴![]()
∴![]() =2
=2![]() =
=![]()


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】(8分)如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断△ABC是直角三角形的是( )
A. a:b:c=3:4:5 B. ∠A:∠B:∠C=3:4:5
C. ∠A+∠B=∠C D. a:b:c=1:2:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于F.
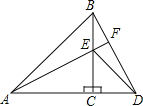
(1)求证:AE=BD;
(2)试判断直线AE与BD的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,![]() ,AC=BC,D为BC的中点,过C作CE⊥AD于点E,延长CE交AB于点F,,连接FD;若AC=4,则CF+FD的值是( )
,AC=BC,D为BC的中点,过C作CE⊥AD于点E,延长CE交AB于点F,,连接FD;若AC=4,则CF+FD的值是( )

A.![]() B.5C.
B.5C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=2x+3与x轴、y轴的交点分别为A、B两点,将直线l1向下平移1个长度单位后得到直线l2,直线l2与x轴交于点C,与y轴交于点D,
(1)求△AOB 的面积;
(2)直线l2的表达式;
(3)求△CBD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方体的长AC=3cm,宽BC=2cm,高AA′=5cm.一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近?最短路程是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点E,若DE=3cm,则AC= ( )

A.9cmB.6cmC.12cmD.3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,M,N分别是OA,OB上的定点,P,Q分别是边OB,OA上的动点,如果记∠AMP=![]() ,∠ONQ=
,∠ONQ=![]() ,当MP+PQ+QN最小时,则
,当MP+PQ+QN最小时,则![]() 与
与![]() 的数量关系是_________________.
的数量关系是_________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com