
【题目】如图,抛物线y= ![]() x2﹣mx+n与x轴交于A、B两点,与y轴交于点C(0,﹣1).且对称轴x=1.
x2﹣mx+n与x轴交于A、B两点,与y轴交于点C(0,﹣1).且对称轴x=1.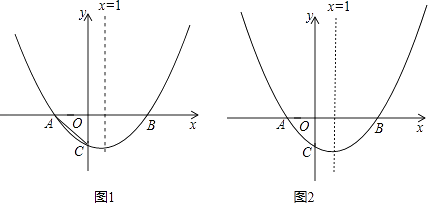
(1)求出抛物线的解析式及A、B两点的坐标;
(2)在x轴下方的抛物线上是否存在点D,使四边形ABDC的面积为3?若存在,求出点D的坐标;若不存在.说明理由(使用图1);
(3)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形,请求出所有满足条件的点P的坐标(使用图2).
【答案】
(1)
解:∵抛物线与y轴交于点C(0,﹣1).且对称轴x=l.
∴  ,解得:
,解得:  ,
,
∴抛物线解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣1,
x﹣1,
令 ![]() x2﹣
x2﹣ ![]() x﹣1=0,得:x1=﹣1,x2=3,
x﹣1=0,得:x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0)
(2)
解:设在x轴下方的抛物线上存在D(a, ![]() )(0<a<3)使四边形ABCD的面积为3.
)(0<a<3)使四边形ABCD的面积为3.
作DM⊥x轴于M,则S四边形ABDC=S△AOC+S梯形OCDM+S△BMD,
∴S四边形ABDC= ![]() |xAyC|+
|xAyC|+ ![]() (|yD|+|yC|)xM+
(|yD|+|yC|)xM+ ![]() (xB﹣xM)|yD|
(xB﹣xM)|yD|
= ![]() ×1×1+
×1×1+ ![]() [﹣(
[﹣( ![]() a2﹣
a2﹣ ![]() a﹣1)+1]×a+
a﹣1)+1]×a+ ![]() (3﹣a)[﹣(
(3﹣a)[﹣( ![]() a2﹣
a2﹣ ![]() a﹣1)]
a﹣1)]
=﹣ ![]() a2+
a2+ ![]() +2,
+2,
∴由﹣ ![]() a2+
a2+ ![]() +2=3,
+2=3,
解得:a1=1,a2=2,
∴D的纵坐标为: ![]() a2﹣
a2﹣ ![]() a﹣1=﹣
a﹣1=﹣ ![]() 或﹣1,
或﹣1,
∴点D的坐标为(1,﹣ ![]() ),(2,﹣1)
),(2,﹣1)

(3)
解:①当AB为边时,只要PQ∥AB,且PQ=AB=4即可,又知点Q在y轴上,所以点P的横坐标为﹣4或4,
当x=﹣4时,y=7;当x=4时,y= ![]() ;
;
所以此时点P1的坐标为(﹣4,7),P2的坐标为(4, ![]() );
);
②当AB为对角线时,只要线段PQ与线段AB互相平分即可,线段AB中点为G,PQ必过G点且与y轴交于Q点,
过点P3作x轴的垂线交于点H,
可证得△P3HG≌△Q3OG,
∴GO=GH,
∵线段AB的中点G的横坐标为1,
∴此时点P横坐标为2,
由此当x=2时,y=﹣1,
∴这是有符合条件的点P3(2,﹣1),
∴所以符合条件的点为:P1的坐标为(﹣4,7),P2的坐标为(4, ![]() );P3(2,﹣1).
);P3(2,﹣1).

【解析】(1)根据二次函数对称轴公式以及二次函数经过(0.﹣1)点即可得出答案;(2)根据S四边形ABDC=S△AOC+S梯形OCDM+S△BMD , 表示出关于a的一元二次方程求出即可;(3)分别从当AB为边时,只要PQ∥AB,且PQ=AB=4即可以及当AB为对角线时,只要线段PQ与线段AB互相平分即可,分别求出即可.
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】某县为鼓励失地农民自主创业,在2010年对60位自主创业的失地农民进行了奖励,共计奖励了10万元.奖励标准是:失地农民自主创业连续经营一年以上的给予1000元奖励:自主创业且解决5人以上失业人员稳定就业一年以上的,再给予2000元奖励.问:该县失地农民中自主创业连续经营一年以上的和自主创业且解决5人以上失业人员稳定就业一年以上的农民分别有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
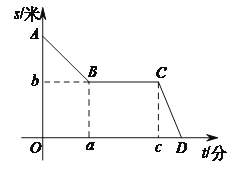
【题目】李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程s(米)与所用时间t(分)之间的关系如图所示.
(1)求a,b,c的值;
(2)求李老师从学校到家的总时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五子棋深受广大棋友的喜爱,其规则是:在 15 15 的正方形棋盘中,由黑方先行,轮流奕子,在任何一方向(横向、竖向或斜线 方向)上连成五子者为胜。如图 3 是两个五子棋爱好者甲和乙的 部分对弈图(甲执黑子先行,乙执白子后走),观察棋盘思考:若 A 点的位置记作(8,4),若不让乙在短时间内获胜,则甲必须落子 的位置是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△AB C沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为( )
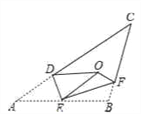
A. 40° B. 41° C. 42° D. 43°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com