
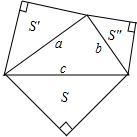
 如图,以直角三角形的三边为斜边向形外作等腰直角三角形,以直角边a,b为斜边的等腰直角三角形面积记为S′和S″,直角三角形的斜边长c为8,则S′+S″=
如图,以直角三角形的三边为斜边向形外作等腰直角三角形,以直角边a,b为斜边的等腰直角三角形面积记为S′和S″,直角三角形的斜边长c为8,则S′+S″=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
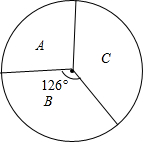 某校对1500名在校学生进行每周上网的情况调查,A为每天上网的学生,B为从不上网的学生,C为偶尔上网的学生,如扇形统计图所示,根据注释,解答以下问题:
某校对1500名在校学生进行每周上网的情况调查,A为每天上网的学生,B为从不上网的学生,C为偶尔上网的学生,如扇形统计图所示,根据注释,解答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:
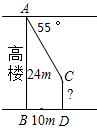 如图,王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为55°,又知水平距离BD=10m,楼高AB=24m,则树高CD等于
如图,王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为55°,又知水平距离BD=10m,楼高AB=24m,则树高CD等于查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com