
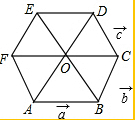
 如图,在正六边形ABCDEF(由六个完全相同的等边三角形拼成)中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.
如图,在正六边形ABCDEF(由六个完全相同的等边三角形拼成)中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.分析 (1)由在正六边形ABCDEF中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$,根据平行四边形法则,可得$\overrightarrow{AF}$=$\overrightarrow{CD}$=$\overrightarrow{c}$,$\overrightarrow{OC}$=$\overrightarrow{FO}$=$\overrightarrow{a}$,然后利用三角形法则求得$\overrightarrow{c}$-($\overrightarrow{a}$+$\overrightarrow{b}$)的值;
(2)在正六边形ABCDEF中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$,根据平行四边形法则,可得$\overrightarrow{BO}$=$\overrightarrow{CD}$=$\overrightarrow{c}$,$\overrightarrow{AO}$=$\overrightarrow{BC}$=$\overrightarrow{b}$,然后利用三角形法则求得答案;
(3)在正六边形ABCDEF中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$,根据平行四边形法则,可得$\overrightarrow{ED}$=$\overrightarrow{AB}$=$\overrightarrow{a}$,然后利用三角形法则求得答案.
解答 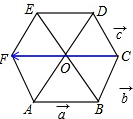 解:(1)∵在正六边形ABCDEF中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$,
解:(1)∵在正六边形ABCDEF中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$,
∴$\overrightarrow{AF}$=$\overrightarrow{CD}$=$\overrightarrow{c}$,$\overrightarrow{OC}$=$\overrightarrow{FO}$=$\overrightarrow{a}$,
∴$\overrightarrow{CF}$=2$\overrightarrow{a}$,
∴$\overrightarrow{c}$-($\overrightarrow{a}$+$\overrightarrow{b}$)=$\overrightarrow{AF}$-($\overrightarrow{AB}$+$\overrightarrow{BC}$)=$\overrightarrow{AF}$-$\overrightarrow{AC}$=$\overrightarrow{CF}$=2$\overrightarrow{a}$;
如图:
(2)∵在正六边形ABCDEF中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$,
∴$\overrightarrow{BO}$=$\overrightarrow{CD}$=$\overrightarrow{c}$,$\overrightarrow{AO}$=$\overrightarrow{BC}$=$\overrightarrow{b}$,
∴$\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{a}$+$\overrightarrow{c}$-$\overrightarrow{b}$=$\overrightarrow{AB}$+$\overrightarrow{BO}$-$\overrightarrow{AO}$=$\overrightarrow{AO}$-$\overrightarrow{AO}$=$\overrightarrow{0}$;
(3)∵在正六边形ABCDEF中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$,
∴$\overrightarrow{ED}$=$\overrightarrow{AB}$=$\overrightarrow{a}$,
∴$\overrightarrow{BE}$=$\overrightarrow{BC}$+$\overrightarrow{CD}$+$\overrightarrow{DE}$=$\overrightarrow{b}$+$\overrightarrow{c}$-$\overrightarrow{a}$.
点评 此题考查了平面向量的知识.注意掌握平行四边形法则与三角形法则的应用是解此题的关键.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
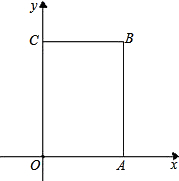 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动.
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
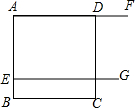 如图,正方形ABCD的边长是4,E是AB上一点,F是AD延长线上的一点,BE=DF,四边形AEGF是矩形,矩形AEGF的面积y随BE的长x的变化而变化,y与x之间的关系可以用怎样的函数来表示?
如图,正方形ABCD的边长是4,E是AB上一点,F是AD延长线上的一点,BE=DF,四边形AEGF是矩形,矩形AEGF的面积y随BE的长x的变化而变化,y与x之间的关系可以用怎样的函数来表示?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
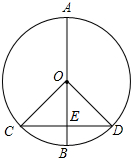 如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )
如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )| A. | ∠AOC=∠AOD | B. | BE=OE | C. | CE=DE | D. | AC=AD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
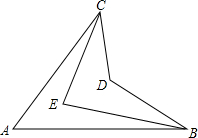 如图,若∠ACE=$\frac{1}{3}$∠ACD,∠ABE=$\frac{1}{3}$∠ABD,猜想∠A,∠CEB和∠CDB之间的数量关系为2∠A+∠CDB=3∠CEB.(写出结论,不必证明)
如图,若∠ACE=$\frac{1}{3}$∠ACD,∠ABE=$\frac{1}{3}$∠ABD,猜想∠A,∠CEB和∠CDB之间的数量关系为2∠A+∠CDB=3∠CEB.(写出结论,不必证明)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com