
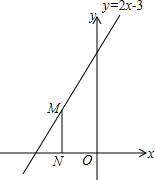
 如图,点M是直线y=2x+3上的动点,过点M作MH⊥x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形?小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,△MNP为等腰直角三角形,请你写出y轴上其它M在x轴上方点P的坐标(0,0),(0,$\frac{3}{4}$),(0,1).
如图,点M是直线y=2x+3上的动点,过点M作MH⊥x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形?小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,△MNP为等腰直角三角形,请你写出y轴上其它M在x轴上方点P的坐标(0,0),(0,$\frac{3}{4}$),(0,1). 分析 分两类情况讨论:当MN为直角边时和当MN为斜边时,如图1,当M运动到(-1,1)时,于是得到ON=1,MN=1,根据MN⊥x轴,所以由ON=MN可知(0,0)就是符合条件的一个P点;如图2,又当M运动到第三象限时,根据MN=MP且PM⊥MN,设点M(x,2x+3),列方程解得x=-3,所以点P坐标为(0,-3),由于M在x轴上方,此时点P坐标为(0,-3)不合题意;如若MN为斜边时,根据ON=OP,列方程得到-x=-$\frac{1}{2}$(2x+3),这方程无解,所以这时不存在符合条件的P点;又如图2,当点M′在第二象限,M′N′为斜边时,根据N′P=M′P,∠M′N′P=45°,列方程-x=$\frac{1}{2}$(2x+3),解得x=-$\frac{3}{4}$,这时点P的坐标为(0,$\frac{3}{4}$).
解答 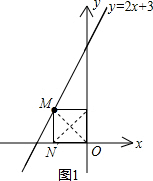 解:如图1,当M运动到(-1,1)时,ON=1,MN=1,
解:如图1,当M运动到(-1,1)时,ON=1,MN=1,
∵MN⊥x轴,所以由ON=MN可知,(0,0)就是符合条件的一个P点;
如图2,又当M运动到第三象限时,要MN=MP,且PM⊥MN,
设点M(x,2x+3),则有-x=-(2x+3),
解得x=-3,所以点P坐标为(0,-3),
∵M在x轴上方,∴此时点P坐标为(0,-3)不合题意;
如若MN为斜边时,则∠ONP=45°,所以ON=OP,设点M(x,2x+3),
则有-x=-$\frac{1}{2}$(2x+3),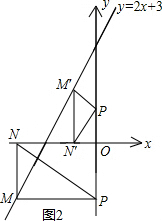
化简得-2x=-2x-3,
这方程无解,所以这时不存在符合条件的P点;
又如图2,当点M′在第二象限,M′N′为斜边时,这时N′P=M′P,∠M′N′P=45°,
设点M′(x,2x+3),则OP=ON′,而OP=$\frac{1}{2}$M′N′,
∴有-x=$\frac{1}{2}$(2x+3),
解得x=-$\frac{3}{4}$,这时点P的坐标为(0,$\frac{3}{4}$).
因此,其他符合条件的点P坐标是(0,0),(0,$\frac{3}{4}$),(0,1).
故答案为:(0,0),(0,$\frac{3}{4}$),(0,1).
点评 本题考查了等腰直角三角形的性质,坐标与图形性质,利用了分类讨论的思想,分类讨论时注意考虑问题要全面,做到不重不漏.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
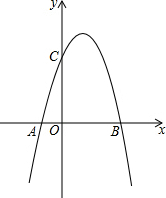 在平面直角坐标系xOy中,已知二次函数y=ax2-2ax+c(a≠0)的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C(0,3),且过点(4,-5).
在平面直角坐标系xOy中,已知二次函数y=ax2-2ax+c(a≠0)的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C(0,3),且过点(4,-5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
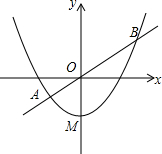 如图,已知抛物线y=x2+bx+c的顶点M的坐标为(0,-1).
如图,已知抛物线y=x2+bx+c的顶点M的坐标为(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
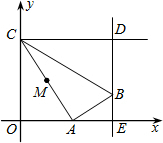 如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=$\frac{25}{4}$时,t的值为( )
如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=$\frac{25}{4}$时,t的值为( )| A. | 2或2+3$\sqrt{2}$ | B. | 2或2+3$\sqrt{3}$ | C. | 3或3+5$\sqrt{3}$ | D. | 3或3+5$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一张纸片的形状为直角三角形,其中∠C=90°,AC=6cm,BC=8cm,沿直线AD折叠该纸片,使直角边AC与斜边上的AE重合,则CD的长为3cm.
如图,一张纸片的形状为直角三角形,其中∠C=90°,AC=6cm,BC=8cm,沿直线AD折叠该纸片,使直角边AC与斜边上的AE重合,则CD的长为3cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
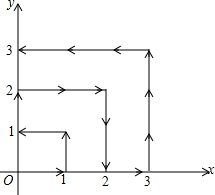 如图,在平面直角坐标系的第一象限内,如果原点是1号点,(1,0)点是2号点,(1,1)点是3号点,(0,1)点是4号点,(0,2)点是5号点,…按箭头所示,第2008号点的坐标是(0,669).
如图,在平面直角坐标系的第一象限内,如果原点是1号点,(1,0)点是2号点,(1,1)点是3号点,(0,1)点是4号点,(0,2)点是5号点,…按箭头所示,第2008号点的坐标是(0,669).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com