练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．用不等号或含绝对值的式子填空．
    （1）若a＞0，b＞0．则a+b＞00，a+b=+（|a|+|b|）；
    （2）若a＜0，b＜0．则a+b＜0，a+b=-（|a|+|b|）；
    （3）若a＞0，b＜0，且|a|＞|b|，则a+b＞0，a+b=+（|a|-|b|）；
    （4）若a＞0，b＜0，且|a|＜|b|，则a+b＜0，a+b=-（|b|-|a|）．

    分析 （1）根据有理数的加法：两正数相加得正，绝对值相加，可得答案；
    （2）根据有理数的加法：两负数相加得负，绝对值相加，可得答案；
    （3）异号两数相加取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值，可得答案；
    （4）异号两数相加取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值，可得答案．

    解答 解：（1）若a＞0，b＞0．则a+b＞0，a+b=+（|a|+|b|）；
    （2）若a＜0，b＜0．则a+b＜0，a+b=-（|a|+|b|）；
    （3）若a＞0，b＜0，且|a|＞|b|，则a+b＞0，a+b=+（|a|-|b|）；
    （4）若a＞0，b＜0，且|a|＜|b|，则a+b＜0，a+b=-（|b|-|a|），
    故答案为：＞，+（|a|+|b|）；＜，-（|a|+|b|）；＞，+（|a|-|b|）；＜，-（|b|-|a|）．

    点评 本题考查了有理数的加法，利用了有理数的加法运算，熟记法则并根据法则计算是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

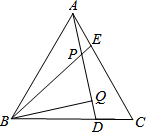    9．已知，如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD于Q，PQ=3，PE=1．
    （1）求证：△ABE≌△CAD；
    （2）求∠BPQ的度数；
    （3）求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．先化简，再求值：
    （1）（x+2）（x-2）+x（1-x），其中x=$\sqrt{2}$
    （2）先化简再求值：（2a-1）2+2（2a+1），其中a=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．要使式子$\sqrt{2x-5}$有意义，字母x的取值必须满足x≥$\frac{5}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先化简，再求值：$\frac{2y}{{x}^{2}-{y}^{2}}$-$\frac{1}{x-y}$，其中x=3$\sqrt{2}$-2，y=-2$\sqrt{2}$+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知$\frac{{x}^{2}+1}{x}$=$\sqrt{5}$，求$\frac{{x}^{4}+{x}^{2}+1}{{x}^{4}-{x}^{2}+1}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，已知点A的坐标是（-1，0），点B的坐标是（9，0），以AB为直径作⊙O′，交y轴的负半轴于点C，连接AC、BC，过A、B、C三点作抛物线．
    （1）求抛物线的解析式；
    （2）点E是AC延长线上一点，∠BCE的平分线CD交⊙O′于点D，连结BD，求直线BD的解析式；
    （3）在（2）的条件下，抛物线上是否存在点P，使得∠PDB=∠CBD？如果存在，请求出点P的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，AD为△ABC的中线，BE为△ABD的中线．
    （1）在△BED中作BD边上的高，垂足为F；
    （2）若△ABC的面积为40，BD=5，则△BDE中BD边上的高为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

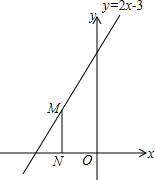    5．如图，点M是直线y=2x+3上的动点，过点M作MH⊥x轴于点N，y轴上是否存在点P，使△MNP为等腰直角三角形？小明发现：当动点M运动到（-1，1）时，y轴上存在点P（0，1），此时有MN=MP，△MNP为等腰直角三角形，请你写出y轴上其它M在x轴上方点P的坐标（0，0），（0，$\frac{3}{4}$），（0，1）．

    查看答案和解析>>

    同步练习册答案