
【题目】如图,已知抛物线![]() 与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且
与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C,求![]() 面积的最大值;
面积的最大值;
(3)在(2)中![]() 面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)4;(3)存在,Q的坐标为
;(2)4;(3)存在,Q的坐标为![]() 或
或![]()
【解析】
![]() 根据题意将
根据题意将![]() 、
、![]() 的坐标代入抛物线表达式,即可求解;
的坐标代入抛物线表达式,即可求解;
![]() 由题意设点M的坐标为
由题意设点M的坐标为![]() ,则点
,则点![]() ,
,![]() ,即可求解;
,即可求解;
![]() 由题意和如图所示可知,
由题意和如图所示可知,![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,进行分析计算即可求解.
,进行分析计算即可求解.
解:![]() 将
将![]() 、
、![]() 的坐标代入抛物线表达式得:
的坐标代入抛物线表达式得:![]() ,解得:
,解得:![]() ,
,
则抛物线的解析式为:![]() ;
;
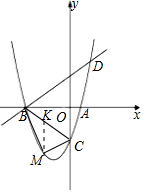
![]() 过点M作y轴的平行线,交直线BC于点K,
过点M作y轴的平行线,交直线BC于点K,
将点B、C的坐标代入一次函数表达式:![]() 得:
得:![]() ,解得:
,解得: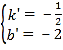 ,
,
则直线BC的表达式为:![]() ,
,
设点M的坐标为![]() ,则点
,则点![]() ,
,
![]() ,
,
![]() ,
,![]() 有最大值,
有最大值,
当![]() 时,
时,
![]() 最大值为4,
最大值为4,
点M的坐标为![]() ;
;
![]() 如图所示,存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆,切点为N,
如图所示,存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆,切点为N,
过点M作直线平行于y轴,交直线AC于点H,
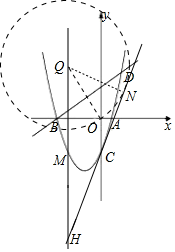
点M坐标为![]() ,设:点Q坐标为
,设:点Q坐标为![]() ,
,
点A、C的坐标为![]() 、
、![]() ,
,![]() ,
,
![]() 轴,
轴,
![]() ,
,
![]() ,则
,则![]() ,
,
将点A、C的坐标代入一次函数表达式:![]() 得:
得:![]() ,
,
则直线AC的表达式为:![]() ,
,
则点![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
解得:![]() 或
或![]() ,
,
即点Q的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】实行垃圾资源化利用,是社会文明水平的一个重要体现.某环保公司研发的甲、乙两种智能设备可利用最新技术将干垃圾变身为燃料棒.某垃圾处理厂从环保公司购入以上两种智能设备,若干已知购买甲型智能设备花费360万元,购买乙型智能设备花费480万元,购买的两种设备数量相同,且两种智能设备的单价和为140万元.
(1)求甲乙两种智能设备单价;
(2)垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的40%,且生产每吨燃料棒所需人力成本比物资成本的![]() 倍还多10元,调查发现:若燃料棒售价为每吨200元,平均每天可售出350吨,而当销售价每降低1元,平均每天可多售出5吨,但售价在每吨200元基础上降价幅度不超过7%,
倍还多10元,调查发现:若燃料棒售价为每吨200元,平均每天可售出350吨,而当销售价每降低1元,平均每天可多售出5吨,但售价在每吨200元基础上降价幅度不超过7%,
①垃圾处理厂想使这种燃料棒的销售利润平均每天达到36080元,求每吨燃料棒售价应为多少元?
②每吨燃料棒售价应为多少元时,这种燃料棒平均每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一块含30°(即∠CAB=30°)角的三角板和一个量角器拼在一起,三角板斜边AB与量角器所在圆的直径MN恰好重合,其量角器最外缘的读数是从N点开始(即N点的读数为0°),现有射线CP绕点C从CA的位置开始按顺时针方向以每秒2度的速度旋转到CB位置,在旋转过程中,射线CP与量角器的半圆弧交于E.

(1)当旋转7.5秒时,连接BE,试说明:BE=CE;
(2)填空:①当射线CP经过△ABC的外心时,点E处的读数是 .
②当射线CP经过△ABC的内心时,点E处的读数是 ;
③设旋转x秒后,E点出的读数为y度,则y与x的函数式是y= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某核桃种植基地计划种植![]() 、
、![]() 两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.设该基地种植了
两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.设该基地种植了![]() 种核桃
种核桃![]() 亩.
亩.
(Ⅰ)若该基地收获两种核桃的年总产量为25 800千克,则![]() 、
、![]() 两种核桃各种植了多少亩?
两种核桃各种植了多少亩?
(Ⅱ)全部收购后,总收入为![]() 元,求出
元,求出![]() 与
与![]() 之间的函数关系式.若要求种植
之间的函数关系式.若要求种植![]() 种核桃的面积不少于
种核桃的面积不少于![]() 种核桃的一半,那么种植
种核桃的一半,那么种植![]() 种核桃多少亩时,该种植基地的总收入最多?最多是多少元?
种核桃多少亩时,该种植基地的总收入最多?最多是多少元?
解:(Ⅰ)先用含![]() 的代数式填空,再完成解答.
的代数式填空,再完成解答.
由种植了![]() 种核桃
种核桃![]() 亩,可知
亩,可知![]() 种核桃种植的亩数为________,则
种核桃种植的亩数为________,则![]() 种核桃的年总产量为________千克,
种核桃的年总产量为________千克,![]() 种核桃的年总产量为________千克.
种核桃的年总产量为________千克.
根据题意列出方程________________________;
解得:
(Ⅱ)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△BED都是等腰直角三角形,∠ABC=∠DBE=90°,AD,CE相交于点G
(1)求证:△ABD≌△CBE;
(2)求证:AD⊥CE;
(3)连接AE,CD,若AE=![]() CD=5,求△ABC和△BED的面积之和.
CD=5,求△ABC和△BED的面积之和.
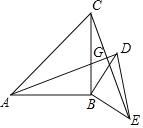
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现)
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①).
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?请证明点D也不在⊙O内.
(应用)
利用(发现)和(思考)中的结论解决问题:
(1)如图④,已知∠BCD=∠BAD,∠CAD=40°,求∠CBD的度数.
(2)如图⑤,若四边形ABCD中,∠CAD=90°,作∠CDF=90°,交CA延长线于F,点E在AB上,∠AED=∠ADF,CD=3,EC=2,求ED的长.
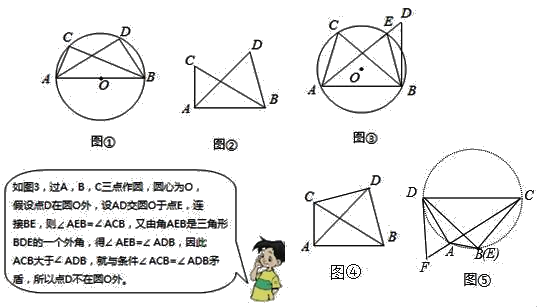
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BDE中,∠BDE=90°,BD=4,点D的坐标是(6,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为__________.
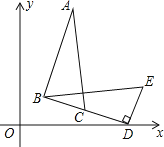
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行趣味运动会共有三个项目:A.“协力竞走”、B.“快乐接力”、C.“摸石过河”.小明和小刚参与了该运动会的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到A.“协力竞走”项目组的概率为 ;
(2)列表或画树状图求小明和小刚被分配到同一项目组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查,问卷给出了四种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的扇形统计图和条形统计图(均不完整).

根据以上信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生;
(2)补全条形统计图;
(3)如果全校有1200名学生,学习准备的400个自行车停车位是否够用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com