
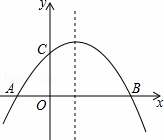
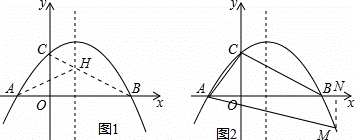
如图,已知抛物线y= ﹣
﹣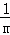 (x+2)(x﹣m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.
(x+2)(x﹣m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.
(1)若抛物线过点G(2,2),求实数m的值;
(2)在(1)的条件下,解答下列问题:
①求出△ABC的面积;
②在抛物线的对称轴上找一点H,使AH+CH最小,并求出点H的坐标;
(3)在第四现象内,抛物线上是否存在点M,使得以点A、B、M为顶点的三角形与△ACB相似?若存在,求m的值;若不存在,请说明理由.
解:(1)∵抛物线过G(2,2),
∴把G坐标代入抛物线解析式得:2=﹣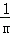 (2+2)(2﹣m),
(2+2)(2﹣m),
解得:m=4;
(2)①令y=0,得到﹣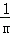 (x+2)(x﹣m)=0,
(x+2)(x﹣m)=0,
解得:x1=﹣2,x2=m,
∵m>0,
∴A(﹣2,0),B(m,0),
把m=4代入得:B(4,0),
∴AB=6,
令x=9,得到y=2,即C(0,2),
∴OC=2,
则S△ABC=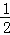 ×6×2=6;
×6×2=6;
②∵A(﹣2,0),B(4,0),
∴抛物线解析式为y=﹣ (x+2)(x﹣4)的对称轴为x=1,
(x+2)(x﹣4)的对称轴为x=1,
如图1,连接BC交对称轴于点H,由对称轴的性质和两点之间线段最短的性质可得:此时AH+CH=BH+CH=BC最小,
设直线BC的解析式为y=kx+b,
把B与C坐标代入得: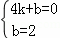 ,
,
解得: ,
,
∴直线BC解析式为y=﹣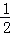 x+2,
x+2,
令x=1,得到y=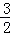 ,即H(1,
,即H(1,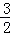 );
);
(3)在第 四现象内,抛物线上存在点M
四现象内,抛物线上存在点M ,使得以点A、B、M为顶点的三角形与△ACB相似,
,使得以点A、B、M为顶点的三角形与△ACB相似,
分两种情况考虑:
(i)当△ACB∽△ABM时,则有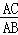 =
=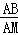 ,即AB2=AC•AM,
,即AB2=AC•AM,
∵A(﹣2,0),C(0,2),即OA=OC=2,
∴∠CAB=45°,∠BAM=45°,
如图2,过M作MN⊥x轴,交x轴于点N,则AN=MN,
∴OA+ON=2+ON=MN,
设M(x,﹣x﹣2)(x>0),
把M坐标代入抛物线解析式得:﹣x﹣2=﹣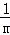 (x+2)(x﹣m),
(x+2)(x﹣m),
∵x>0,∴x+2>0,
∵m>0,∴x=2m,即M(2m,﹣2m﹣2),
∴AM=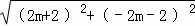 =2
=2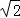 (m+1),
(m+1),
∵AB2=AC•AM,AC=2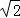 ,AB=m+2,
,AB=m+2,
∴(m+2)2=2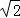 •2
•2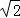 (m+1),
(m+1),
解得:m=2±2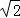 ,
,
∵m>0,
∴m=2+2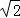 ;
;
(ii)当△ACB∽△MBA时,则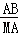 =
=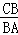 ,即AB2=CB•MA,
,即AB2=CB•MA,
∵∠CBA=∠BAM,∠ANM=∠BOC=90°,
∴△ANM∽△BOC,
∴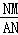 =
=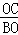 ,
,
∵OB=m,设ON=x,
∴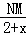 =
= ,即MN=
,即MN= (x+2),
(x+2),
令M(x,﹣ (x+2))(x>0),
(x+2))(x>0),
把M坐标代入抛物线解析式得:﹣ (x+2)=﹣
(x+2)=﹣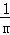 (x+2)(x﹣m),
(x+2)(x﹣m),
∵x>0,∴x+2>0,
∵m>0,∴x=m+2,即M(m+2,﹣ (m+4)),
(m+4)),
∵AB2=CB•MA,CB=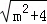 ,AN=m+4,MN=
,AN=m+4,MN=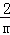 (m+4),
(m+4),
∴(m+2)2=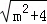 •
•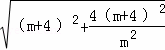 ,
,
整理得: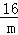 =0,显然不成立,
=0,显然不成立,
综上,在第四象限内,当m=2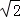 +2时,抛物线上存在点M,使得以点A、B、M为顶点的三角形与△ACB相似.
+2时,抛物线上存在点M,使得以点A、B、M为顶点的三角形与△ACB相似.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
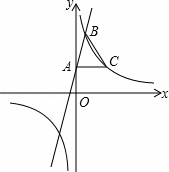
如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y= (k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=
(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y= (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.
(1)求反比例函数的表达式.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
图1是某中学九年级一班全体学生对三种水果喜欢人数的频数分布 统计图,根据图中信息回答下列问题:
统计图,根据图中信息回答下列问题:
(1)九年级一班总人数是多少人?
(2)喜欢哪种水果人数的频数最低?并求出该频率;
(3)请根据频数分布统计图(图1)的数据,补全扇形统计图(图2);
(4)某水果摊位上正好只摆放有这三种水果出售,王阿姨去购买时,随机购买其中两种水果,恰好买到樱桃和枇杷的概率是多少?用树状图或列表说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题正确的是( )
|
| A. | 矩形的对角线互相垂直 |
|
| B. | 两边和一角对应相等的两个三角形全等 |
|
| C. | 分式方程 |
|
| D. | 多项式t2﹣16+3t因式分解为(t+4)(t﹣4)+3t |
查看答案和解析>>
科目:初中数学 来源: 题型:
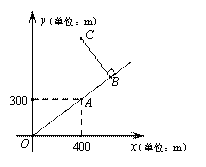
如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com