
����Ŀ�������ij�Ƽ�������˾���Ƴ�һ�����͵IJ�Ʒ��ÿ����Ʒ�ijɱ�Ϊ1200Ԫ�����۵��۶�Ϊ1700Ԫ���ڸò�Ʒ�������ڼ䣬Ϊ�˴����������̼ҹ�������Ͳ�Ʒ����˾�����̼�һ�ι����������Ͳ�Ʒ������10��ʱ��ÿ����1700Ԫ���ۣ���һ�ι�����ֲ�Ʒ����10��ʱ��ÿ���һ�����������ȫ����Ʒ�����۵��۾�����10Ԫ�������۵��۾�������1400Ԫ��
��1�����˿�һ�ι������ֲ�Ʒ6��ʱ����˾����õ�����Ϊ Ԫ��
��2���˿�һ���Թ���ò�Ʒ���ٶ��ټ�ʱ�������۵���Ϊ1400Ԫ��
��3�������г����飬�ù�˾��������Ա���֣���һ���Թ����Ʒ�ļ�������ijһ����ʱ�����������һ�ι�������������࣬��˾����õ�����������һ�������һ���Թ���ò�Ʒx������˾����õ�����ΪyԪ
������ͨ�����������ʱy��Ԫ����x������֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��Ϊʹ�˿�һ���Թ��������Խ�࣬��˾����õ�����Խ��˾Ӧ��������۵��۵���Ϊ Ԫ�������������������䣩
���𰸡���1��3000����2��40������3����y= ����1500.
����1500.
��������
��1��������y=�����۵���-�ɱ����ۣ����������ɵõ����ۣ�
��2�������Ϊx�������۵���Ϊ1700-10��x-10��Ԫ���������۵���ǡ��Ϊ1400Ԫ���з�����⣻
��3����������y=�����۵���-�ɱ����ۣ��������������۵��۾�������2600Ԫ����0��x��10��10��x��50��x��50��������г�������ϵʽ��
���ɢٵĺ�����ϵʽ�����ö��κ�������������������ֵ����������ֵʱx��ֵ��ȷ�����۵��ۣ�
��1����6��10��
�ࣨ1700-1200����6=3000Ԫ��
�𣺹˿�һ�ι������ֲ�Ʒ6��ʱ����˾����õ�����Ϊ3000Ԫ��
��2�������Ϊx�������⣬��
1700-10��x-10��=1400��
���x=40��
���̼�һ�ι������ֲ�Ʒ40��ʱ�����۵���ǡ��Ϊ1400Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ij�ز�ר��������һ�����棬ÿǧ�˵Ľ���Ϊ10Ԫ�����۹����з��֣�ÿ������![]() �����۵���x��Ԫ��֮���ϵ���Խ��Ƶؿ���һ�κ���
�����۵���x��Ԫ��֮���ϵ���Խ��Ƶؿ���һ�κ���![]() .������=�ۼ�-���ۣ�
.������=�ۼ�-���ۣ�
��1��д��ÿ�������w��Ԫ�������۵���x��Ԫ��֮�亯������ʽ��
��2�������۵��۶�Ϊ����Ԫʱ����������ÿ���ܹ�������������������Ƕ���Ԫ��
��3����۲��Ź涨��������������۵��۲��ø���30Ԫ.���̵���Ҫ��������ÿ����300Ԫ�����������۵���Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���д�С���ֻ�����3���������4��С����һ�ο����˻�18�֣�2���������6��С����һ�ο����˻�17��.
��1������1���������1��С����һ�ο��Էֱ��˻����ٶ֣�
��2��Ŀǰ��33�ֻ�����Ҫ���䣬���˹�˾�ⰲ�Ŵ�С��������10����ȫ������һ�����꣬����ÿ�������һ���˷ѻ���130Ԫ��ÿ��С����һ���˻�����100Ԫ�����ʻ��˹�˾Ӧ��ΰ��ų������ʡ���ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017�㽭ʡ�����У���23�⣬10�֣�������������֮��֮�ƣ�ijˮ����ֳ��Ϊ�˸��õط��Ӽ������ƣ�һ�����չ���20000kg��ˮ�㣬�ƻ���ֳһ��ʱ����ٳ��ۣ���֪ÿ������ķ�����ͬ������10����ܳɱ�Ϊ30.4��Ԫ������20����ܳɱ�Ϊ30.8��Ԫ���ܳɱ�=�����ܷ���+�չ��ɱ�����
��1����ÿ��ķ���������a��Ԫ���չ��ɱ�Ϊb��Ԫ����a��b��ֵ��
��2����������ˮ�����t��������Ϊm��kg�������۵���ΪyԪ/kg���������������֪��m��t�ĺ�����ϵΪ![]() ��y��t�ĺ�����ϵ��ͼ��ʾ��
��y��t�ĺ�����ϵ��ͼ��ʾ��
�ٷֱ������0��t��50��50��t��100ʱ��y��t�ĺ�����ϵʽ��
���轫������ˮ�����t���һ���Գ�����������ΪWԪ����tΪ��ֵʱ��W���������ֵ��������=�����ܶ�ܳɱ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵxOy�У�������y=![]() ��y�ύ�ڵ�A������ΪB��ֱ��l��y=-
��y�ύ�ڵ�A������ΪB��ֱ��l��y=-![]() x+b������A���������ߵĶԳ��ύ�ڵ�C����P�ǶԳ����ϵ�һ�����㣬��AP+
x+b������A���������ߵĶԳ��ύ�ڵ�C����P�ǶԳ����ϵ�һ�����㣬��AP+![]() PC��ֵ��С�����P������Ϊ�� ��
PC��ֵ��С�����P������Ϊ�� ��
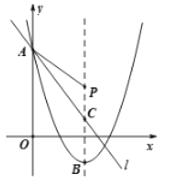
A. ��3��1��
B. ��3��![]() ��
��
C. ��3��![]() ��
��
D. ��3��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ3��������ֽƬABCD���ۣ�ʹAB��DC�غϣ��ۺ�ΪEF��չƽ���ٽ���B�۵���CD�ϣ�ʹ��AB������E���ۺ�ΪGH����B�Ķ�Ӧ��ΪM����A�Ķ�Ӧ��ΪN����ô�ۺ�GH�ij�Ϊ_____��
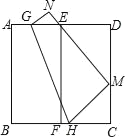
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����¥AC��һ����һ��б�£�б�µ��½�Ϊ30�㣮С���ڴ�¥��B���������ײ�E���ĸ���Ϊ33�㣬��¥��A���������D���ĸ���Ϊ30�㣮��֪����DE��20m��CE��30m����C��D��E��ͬһƽ���ڣ���A��B����֮��ľ��룮�������ȷ��1m���ο����ݣ�![]() ��1.73��sin33���0.54��cos33���0.84��tan33���0.65��
��1.73��sin33���0.54��cos33���0.84��tan33���0.65��
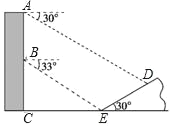
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����AOB�͡�COD��Ϊ����ֱ�������Σ���AOB����COD��90�㣬AO��4��CO��2��������AD��BC����HΪBC�е㣬����OH��
��1����ͼ1��ʾ����֤��OH��![]() AD��OH��AD��
AD��OH��AD��
��2������COD�Ƶ�O��ת��ͼ2��ʾλ��ʱ���߶�OH��AD���������Ĺ�ϵ��֤����Ľ��ۣ�
��3����ֱ��д���߶�OH��ȡֵ��Χ��
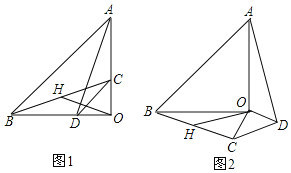
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Rt��ABC�У���C��90������ABC��30����AC��1����Rt��ABC�Ƶ�A��ʱ����ת15���õ�Rt��AB'C'�����е�B�˶���·��Ϊ��BB'����ôͼ����Ӱ���ֵ������_____��
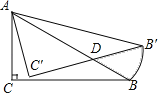
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com