
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB. 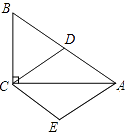
(1)证明:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
【答案】
(1)证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形,
又∵∠ACB=90°,D是AB的中点,
∴CD= ![]() AB=BD=AD,
AB=BD=AD,
∴平行四边形ADCE是菱形
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
∴∠BDC=∠BCD=60°,CD=BC=6,
∵CE∥AB,
∴∠DCE=∠BDC=60°,
又∵CD=BC=6,
∴在Rt△CDF中,DF=CDsin60°=6× ![]() =3
=3 ![]() .
.
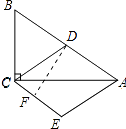
【解析】(1)先证明四边形ADCE是平行四边形,再证出一组邻边相等,即可得出结论;(2)过点D作DF⊥CE,垂足为点F;先证明△BCD是等边三角形,得出∠BDC=∠BCD=60°,CD=BC=6,再由平行线的性质得出∠DCE=∠BDC=60°,在Rt△CDF中,由三角函数求出DF即可.


科目:初中数学 来源: 题型:
【题目】长城公司为希望小学捐赠甲、乙两种品牌的体育器材,甲品牌有A、B、C三种型号,乙品牌有D、E两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.
(1)写出所有的选购方案(用列表法或树状图);
(2)如果在上述选购方案中,每种方案被选中的可能性相同,那么A型器材被选中的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你用学习“一次函数”时积累的经验和方法解决下列问题:
(1)在平面直角坐标系中,画出函数y=|x|的图象;
①列表填空:
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | … |
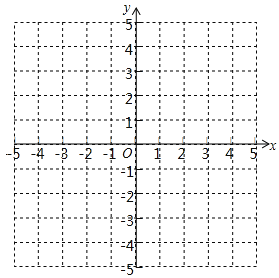
②描点、连线,在图所示的平面直角坐标系中画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|的两条不同类型的性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )


A. 两人从起跑线同时出发,同时到达终点
B. 小苏跑全程的平均速度大于小林跑全程的平均速度
C. 小苏前15s跑过的路程大于小林前15s跑过的路程
D. 小林在跑最后100m的过程中,与小苏相遇2次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( ) 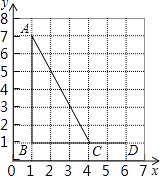
A.(6,0)
B.(6,3)
C.(6,5)
D.(4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家到图书馆看报,然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,试求:
(1)小明回家的速度.
(2)小明离家50分钟时离家的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(﹣3,0)和B(1,0),与y轴交于点C,
(1)求抛物线的表达式;
(2)若点D为此抛物线上位于直线AC上方的一个动点,当△DAC的面积最大时,求点D的坐标;
(3)设抛物线顶点关于y轴的对称点为M,记抛物线在第二象限之间的部分为图象G.点N是抛物线对称轴上一动点,如果直线MN与图象G有公共点,请结合函数的图象,直接写出点N纵坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2022年将在北京﹣﹣张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市,某校开设了冰球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位:cm)如表所示:
队员1 | 队员2 | 队员3 | 队员4 | 队员5 | 队员6 | |
甲组 | 176 | 177 | 175 | 176 | 177 | 175 |
乙组 | 178 | 175 | 170 | 174 | 183 | 176 |
设两队队员身高的平均数依次为 ![]() 甲 ,
甲 , ![]() 乙 , 方差依次为S甲2 , S乙2 , 下列关系中正确的是( )
乙 , 方差依次为S甲2 , S乙2 , 下列关系中正确的是( )
A.![]() 甲=
甲= ![]() 乙 , S甲2<S乙2
乙 , S甲2<S乙2
B.![]() 甲=
甲= ![]() 乙,S甲2>S乙2
乙,S甲2>S乙2
C.![]() 甲<
甲< ![]() 乙 , S甲2<S乙2
乙 , S甲2<S乙2
D.![]() 甲>
甲> ![]() 乙 , S甲2>S乙2
乙 , S甲2>S乙2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com