【题目】如图，矩形
中，
，
，E是边
的中点，点P在边
上，设
，若以点D为圆心，
为半径的
与线段
只有一个公共点，则所有满足条件的x的取值范围是______．
【答案】x=
或
【解析】
根据题意，当
与AE相切时，由相似三角形的性质，可得：
，从而求出x的值，当过点E时，x=PD=DE，当过点A时，x=PD=AD，进而求出x满足的条件.
如图1，当与AE相切时，设切点为G，连接DG，
∵
，
∴DG=DP=x，
∵∠DAG=∠AEB，∠AGD=∠B=90°，
∴AGD~EBA，
∴，
∴
，解得：x=，
如图2，当过点E时，与线段AE有两个公共点，连接DE，此时，PD=DE=5，
∴x=PD=5
如图3，当过点A时，与线段AE有1个公共点，此时，PD=AD=6，
∴x=PD=6，
综上所述：当与线段AE只有一个公共点时，x满足的条件是：x=或；
故答案是：x=或.
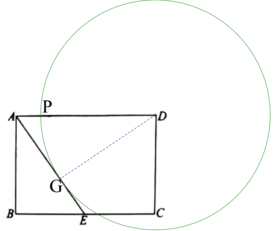
图1 图2
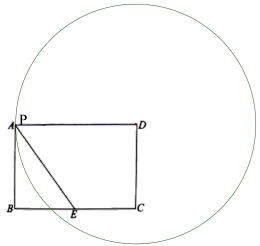
图3
科目：初中数学 来源： 题型：
【题目】某民俗旅游村为接待游客住宿需要，开设了有100张床位的旅馆．当每张床位每天收费100元时，床位可全部租出．若每张床位每天收费提高20元，则相应地减少了10张床位租出．如果每张床位每天以20元为单位提高收费，为使租出的床位少且租金高，那么每张床位每天最合适的收费是( )
A. 140元 B. 150元 C. 160元 D. 180元
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】经过某十字路口的汽车，可能直行，也可能向左转或向右转．如果这三种可能性大小相同，现有两辆汽车经过这个十字路口．
（1）用画树状图法或列表法分析这两辆汽车行驶方向所有可能的结果；
（2）求一辆车向右转，一辆车向左转的概率；
（3）求至少有一辆车直行的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，D、E分别是AB、AC的中点，若△ABC的面积为S△ABC＝36cm2，则梯形EDBC的面积SEDBC为（ ）
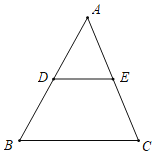
A.9B.18C.27D.30
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）直线l1：y＝x+1与x轴交于点A，直线l2：y＝﹣x+3与x轴交于点B，l1与l2交于点C，直线l3过线段AB的中点和点C，求直线l3的解析式；
（2）已知平面直角坐标系中，直线l经过点P（2，1）且与双曲线y＝
交于A、B不同两点，问是否存在这样的直线l，使得点P恰好为线段AB的中点，若存在，求出直线l的解析式，若不存在，请说明理由；
（3）若A（x1，y1）、B（x2，y2）是抛物线y＝4x2上的不同两点（y1≠y2），线段AB的垂直平分线与y轴交于点P，与线段AB交于点M（xm，ym），则称线段AB为点P的一条“相关弦”，若点P的坐标为（0，a）时（a为常数），证明点P的“相关弦”中点M的纵坐标相同．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P是半圆
弧上一动点，连接AP，作∠APC=45°，交弦AB于点C．AB=6cm．小元根据学习函数的经验，分别对线段AP，PC，AC的长度进行了测量．下面是小元的探究过程，请补充完整：
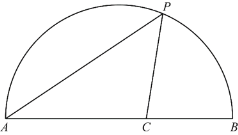
（1）下表是点P是上的不同位置，画图、测量，得到线段AP，PC，AC长度的几组值，如下表：
①经测量m的值是（保留一位小数）．
②在AP，PC，AC的长度这三个量中，确定 的长度是自变量， 的长度和的长度都是这个自变量的函数；
（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数图象；
（3）结合函数图象，解决问题：当△ACP为等腰三角形时，AP的长度约为 cm（保留一位小数）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读对学生的成长有着深远的影响，某中学为了解学生每周课余阅读的时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下不完整的统计图表．
组别 | 时间（小时） | 频数（人数） | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息，解答下列问题：
（1）表中的a= ，b= ，中位数落在 组，将频数分布直方图补全；
（2）估计该校2000名学生中，每周课余阅读时间不足0.5小时的学生大约有多少名？
（3）E组的4人中，有1名男生和3名女生，该校计划在E组学生中随机选出两人向全校同学作读书心得报告，请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y=mx+n(m≠0)的图象与反比例函数y
(k≠0)的图象交于第一、三象限内的A、B两点，与y轴交于点C，过点B作BM⊥x轴，垂足为点M，BM=OM=2，点A的纵坐标为4．
（1）求该反比例函数和一次函数的表达式；
（2）根据图象直接写出当mx+n
时，x的取值范围；
（3）直线AB交x轴于点D，过点D作直线l⊥x轴，如果直线l上存在点P，坐标平面内存在点Q，使以O、P、A、Q为顶点的四边形是矩形，直接写出点P的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
