【题目】如图，在△ABC中，D、E分别是AB、AC的中点，若△ABC的面积为S△ABC＝36cm2，则梯形EDBC的面积SEDBC为（ ）
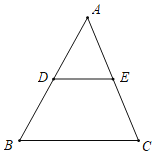
A.9B.18C.27D.30
科目：初中数学 来源： 题型：
【题目】如图1，已知抛物线y＝x2+mx+m﹣1的顶点为D，交y轴于C点，交x轴于A(x1，0)，B(x2，0)两点，点A在y轴左边，点B在y轴右边，且AB＝4．
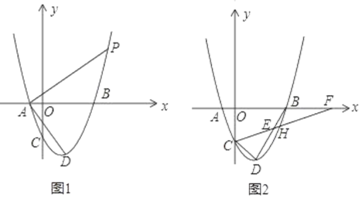
（1）求抛物线的解析式；
（2）如图1，AP⊥AD交抛物线于P．求点P的坐标；
（3）如图2，点H为B，D之间抛物线上一点，直线CH交BD于E，交x轴于F，若S△CDE＝S△BEF，求H点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数
的图象与反比例函数
的图象相交于 A，B 两点，与 x 轴相交于点 C．已知 tan∠BOC=
，点 B 的坐标为（m，n）．
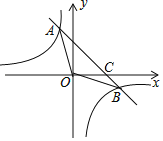
（1）求反比例函数的解析式；
（2）求△AOB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：将函数C1的图象绕点P(m，0)旋转180°，得到新的函数C2的图象，我们称函数C2是函数C1关于点P的相关函数。例如：当m=1时，函数y=(x-3)2+9关于点P(1，0)的相关函数为y=-(x+1)2-9．
（1）当m=0时，
①一次函数y=-x+7关于点P的相关函数为_______；
②点A(5，-6)在二次函数y=ax2-2ax+a(a≠0)关于点P的相关函数的图象上，求a的值；
（2）函数y=(x-2)2+6关于点P的相关函数是y= -(x-10)2-6，则m=_______
（3）当m-1≤x≤m+2时，函数y=x2-6mx+4m2关于点P(m，0)的相关函数的最大值为8，求m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
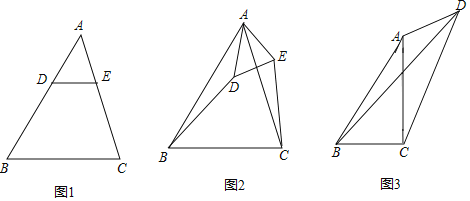
【题目】（1）如图1，在△ABC中，AB＞AC，点D，E分别在边AB，AC上，且DE∥BC，若AD＝2，AE＝
，则
的值是 ；
（2）如图2，在（1）的条件下，将△ADE绕点A逆时针方向旋转一定的角度，连接CE和BD，的值变化吗？若变化，请说明理由；若不变化，请求出不变的值；
（3）如图3，在四边形ABCD中，AC⊥BC于点C，∠BAC＝∠ADC＝θ，且tanθ＝
，当CD＝6，AD＝3时，请直接写出线段BD的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品共50件，已知生产一件A种产品用甲种原料9千克，乙种原料3千克，可获利700元；生产一件B种产品用甲种原料4千克，乙种原料10千克，可获利1200元．
（1）按要求安排A、B两种产品的生产件数，有哪几种方案？请你设计出来；
（2）设生产A、B两种产品总利润为y元，其中一种产品生产件数为x件，试写出y与x之间的函数关系式，并利用函数的性质说明那种方案获利最大？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
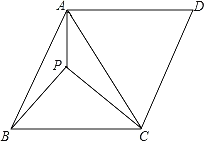
【题目】如图，在菱形ABCD中，∠B＝60°，点P是△ACD内一点，连接PA、PC、PD，若PA＝5，PD＝12，PC＝13，则ACBD＝_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
