
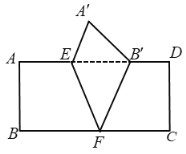
【题目】如图,把矩形![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 边的
边的![]() 处,若
处,若![]() ,
,![]() ,
,![]() ,则矩形
,则矩形![]() 的面积是( )
的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.16
D.16
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
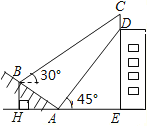
【题目】如图,某大楼的顶部有一块广告牌![]() ,小背在山坡的坡脚
,小背在山坡的坡脚![]() 处测得广告牌底部的仰角为45°,沿坡面
处测得广告牌底部的仰角为45°,沿坡面![]() 向上走到
向上走到![]() 处测得广告牌顶部
处测得广告牌顶部![]() 的仰角为30°.已知山坡
的仰角为30°.已知山坡![]() 的坡度为
的坡度为![]() ,
,![]() 米,
米,![]() 米.
米.
此题考查了折叠的性质、矩形的性质、全等三角形的判定与性质以及勾股定理的应用.熟练掌握折叠的性质是关键.
(1)求点![]() 距地面的高度
距地面的高度![]() ;
;
(2)求广告牌![]() 的高度.(结果保留根号)
的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月,“亚洲文明对话大会”在北京成功举办,某研究机构为了了解10-60岁年年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将搜集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第一组 |
| 5 |
第二组 |
|
|
第三组 |
| 35 |
第四组 |
| 20 |
第五组 |
| 15 |
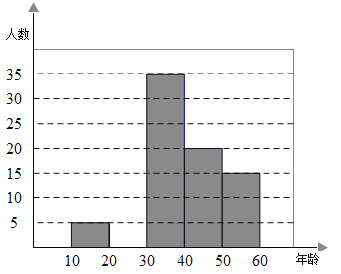

请直接写出第3组人数在扇形统计图中所对应的圆心角是_________度;假设该市现有10-60岁的市民300万人,则40-50岁年龄段的关注本次大会的人数约有___________万人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年某省为加快建设综合交通体系,对铁路、公路、机场三个重大项目加大建设资金的投入.
(1)机场建设项目中所有6个机场投入的建设资金金额统计如下图,已知机场![]() 投入的建设资金金额是机场
投入的建设资金金额是机场![]() 、
、![]() 所投入建设资金金额之和的三分之二,求机场
所投入建设资金金额之和的三分之二,求机场![]() 投入的建设资金金额是多少亿元?并补全条形统计图.
投入的建设资金金额是多少亿元?并补全条形统计图.
(2)将铁路、公路、机场三项建设所投入的资金金额绘制成如下扇形统计图以及统计表,根据扇形统计图及统计表中的信息,求得![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .(请直接填写计算结果)
.(请直接填写计算结果)

铁路 | 公路 | 机场 | 铁路、公路、机场三项投入建设资金总金额(亿元) | |
投入资金(亿元) | 300 |
|
|
|
所占百分比 |
| 34% | 6% | |
所占圆心角 |
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解油价上涨给出租车行业带来的成本压力,某市调整出租车运价,调整方案见下列表格及图象(其中![]() 、
、![]() 、
、![]() 为常数):
为常数):
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超出 | 起步价9元 | 起步价 |
超出 | 每公里2元 | 每公里 |
超出 | 每公里 | |
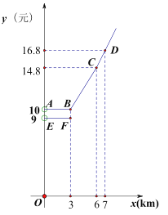
设行驶路程为![]() 时,调价前的运价为
时,调价前的运价为![]() (元),调价后的运价为
(元),调价后的运价为![]() (元).如图,折线
(元).如图,折线![]() 表示
表示![]() 与
与![]() 之间的函数关系;线段
之间的函数关系;线段![]() 表示
表示![]() 时,
时,![]() 与
与![]() 之间的函数关系.根据图表信息,完成下列各题:
之间的函数关系.根据图表信息,完成下列各题:
(1)填空:![]() _____,
_____,![]() _____,
_____,![]() _______;
_______;
(2)写出当![]() 时,
时,![]() 与
与![]() 之间的函数关系式,并在上图中画出该函数图象;
之间的函数关系式,并在上图中画出该函数图象;
(3)当行驶路程为![]() 时,讨论调价前后运价的高低.
时,讨论调价前后运价的高低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,![]() 是正方形
是正方形![]() 边
边![]() 上的一点,连接
上的一点,连接![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,旋转后角的两边分别与射线
,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .写出线段
.写出线段![]() ,
,![]() 和
和![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
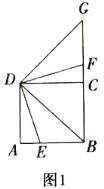
(2)当四边形![]() 为菱形,
为菱形,![]() ,点
,点![]() 是菱形
是菱形![]() 边
边![]() 所在直线上的一点,连接
所在直线上的一点,连接![]() 、
、![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,旋转后角的两边分别与射线
,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
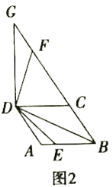
①如图2,点![]() 在线段
在线段![]() 上时,请探究线段
上时,请探究线段![]() ,
,![]() 和
和![]() 之间的数量关系,写出结论并给出证明;
之间的数量关系,写出结论并给出证明;
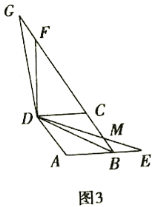
②如图3,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 交射线
交射线![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点P是平行四边形ABCD外一点,PE∥AB交BC于点E.PA、PD分别交BC于点M、N,点M是BE的中点.
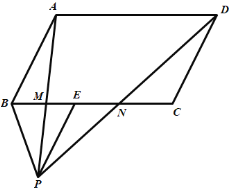
(1)求证:CN=EN;
(2)若平行四边形ABCD的面积为12,求△PMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是弧AB所对弦AB上一动点,过点P作PM⊥AB交AB于点M,连接MB,过点P作PN⊥MB于点N.已知AB =6cm,设A 、P两点间的距离为xcm,P、N两点间的距离为ycm.(当点P与点A或点B重合时,y的值为0)
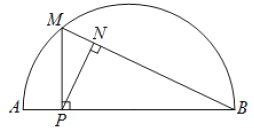
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.0 | 2.3 | 2.1 | 0.9 | 0 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为____________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(5)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如下的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
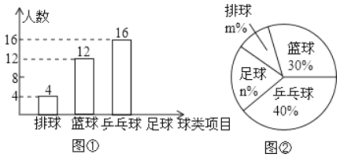
(1)九(5)班的学生人数为_________,并把条形统计图补充完整;
(2)扇形统计图中n=__________,m=___________;
(3)排球兴趣小组4名学生中有2男2女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com