
����Ŀ����ͼ���ڵ�����ABC�У�AC��BC��3![]() ��AB��6����E�ӵ�B��������BA��ÿ��3����λ���ٶ��˶�������E��BC��ƽ���߽���ACB�����ƽ����CF�ڵ�F��
��AB��6����E�ӵ�B��������BA��ÿ��3����λ���ٶ��˶�������E��BC��ƽ���߽���ACB�����ƽ����CF�ڵ�F��
��1����֤���ı���BCFE��ƽ���ı��Σ�
��2������E�DZ�AB���е�ʱ������AF�����ж��ı���AECF����״����˵�����ɣ�
��3�����˶�ʱ��Ϊt�룬�Ƿ����t��ֵ��ʹ���ԡ�EFC����������Ϊ���������ƽ���ı���ǡ�������Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
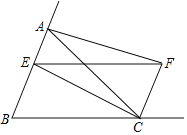
���𰸡���1��֤������������2���ı���AECF�Ǿ��Σ����ɼ���������3��t��ֵΪ![]() ���
���![]() ���2��
���2��
��������
��1���ɵ��������ε����ʵã���B=��BAC�����ɽ�ƽ���߶������������ǵ����ʿɽ��
��2������һ������ֱ�ǵ�ƽ���ı����Ǿ��οɽ��
��3���������������EF=CF����CE=CF����CE=EF���ֱ��з��̿ɽ��
֤������1����ͼ1��
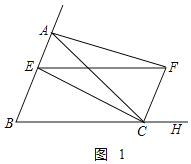
��AC��BC��
���B����BAC��
��CFƽ�֡�ACH��
���ACF����FCH��
�ߡ�ACH����B+��BAC����ACF+��FCH��
���FCH����B��
��BE��CF��
��EF��BC��
���ı���BCFE��ƽ���ı��Σ�
��2���ı���AECF�Ǿ��Σ�
�����ǣ�
��E��AB���е㣬AC��BC��
��CE��AB��
���AEC��90����
�ɣ�1��֪���ı���BCFE��ƽ���ı��Σ�
��CF��BE��AE��
��AE��CF��AE��CF��
���ı���AECF��ƽ���ı��Σ��ҡ�AEC��90����
���ı���AECF�Ǿ��Σ�
��3������EF��CF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����ͼ2��

��BE��BC����3t��3![]() ��
��
��t��![]() ��
��
����CE��CF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����ͼ3����C��CD��AB��D������GC��

��AC��BC��3![]() ��AB��6��
��AB��6��
��BD��AD��3��
�ɹ��ɶ����ã�CD��![]() ��
��![]() ��6��
��6��
���ı���CEGF�����Σ�
��EF��GC����EF��BC��
��GC��BC���ҡ�EGC����ECG��
���EBC����ECB��
��BE��CE��3t��
�ߣ�3t��2��62+��3t��3��2��
��t��![]() ��
��
����CE��EF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����ͼ4��CA��AF��BC����ʱE��A�غϣ�
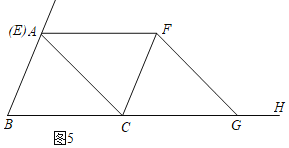
��t��2��
����������t��ֵΪ![]() ���
���![]() ���2�룻
���2�룻



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������̳�����ij����Ʒ��ͳ�Ʒ��֣�ÿ��ӯ��![]() Ԫʱ��ƽ��ÿ�������
Ԫʱ��ƽ��ÿ�������![]() ���������鷢�֣�����Ʒÿ����
���������鷢�֣�����Ʒÿ����![]() Ԫ���̳�ƽ��ÿ��ɶ��۳�
Ԫ���̳�ƽ��ÿ��ɶ��۳�![]() ����
����
![]() �������ڿ����̫���ž����뾡����ٿ�棬�������۸���Ʒ��ӯ���ﵽ
�������ڿ����̫���ž����뾡����ٿ�棬�������۸���Ʒ��ӯ���ﵽ![]() Ԫ�������æ˼�����ý��۶��٣�
Ԫ�������æ˼�����ý��۶��٣�
![]() ���粿�ž��������۸���Ʒ����ӯ���ﵽ��������æ˼�����ָ���ν��ۣ�
���粿�ž��������۸���Ʒ����ӯ���ﵽ��������æ˼�����ָ���ν��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������Լ��,��ƽ��ֱ������ϵ��,����ij����ƽ�����������ƽ������������н�ƽ���ߵ�ֱ��,�иõ������������.����,��M(1��3)���������У�x=1��y=3��y=x+2��y=x+4.��ͼ,��ƽ��ֱ������ϵ����������OABC,��B�ڵ�һ����,A��C�ֱ���x���y����,������![]() ����B.C���㣬����D���������ڲ�.
����B.C���㣬����D���������ڲ�.
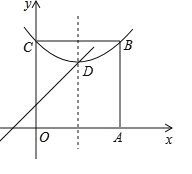
(1)���M��2,3����������������___________________
(2)����D��һ����������y=x+1����������ߵĽ���ʽ________________________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ߵĶ���ΪP��1��4������������y�ύ�ڵ�C��0��3������x�ύ��A��B���㣮
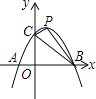
��1����������ߵĽ���ʽ��
��2�����ı���OBPC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ƶ��������Ŀ��ٷ�չ�����ڻ������Ĺ�������Ӧ�˶�����Ϊ�˽�ij��λʹ�ù���������������õ�λ��200��Ա����ij�о�С������ɷ�10λԱ�����õ���10λԱ��һ����ʹ�ù��������Ĵ����ֱ�Ϊ��17��12��15��20��17��0��7��26��17��9��
��1���������ݵ���λ������ ������������ ��
��2������ƽ�������Ƹõ�λԱ��һ����ʹ�ù����������ܴ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016�꣬ijƶ�����ļ�ͥ���˾�������Ϊ2500Ԫ��ͨ��������ҵ���֣���չ����ֳҵ��2018�꣬��ͥ���˾�������ﵽ��3600Ԫ��
��1�����ƶ����2016�굽2018���ͥ���˾����������ƽ�������ʣ�
��2������ƽ�������ʱ��ֲ��䣬2019���ƶ�����ļ�ͥ���˾��������Ƿ��ܴﵽ4200Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2014��1�£����ҷ���ί��ָ̨�������Ҫ��2015���ǰ�����г���ԭ����ȫ��ʵ�о������ˮ���ƶ�. С��Ϊ�˽�����������ˮ�۷�������ᷴ�죬����������Լ���ס��С���IJ��־�����ÿ��ÿ������ˮ�����������۶���ˮ��Ϊ�ı�������������е��飬���ѵ����������������ͼ1��ͼ2.
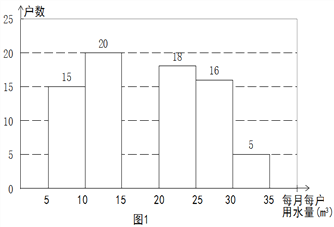
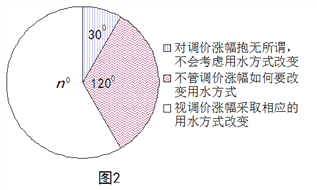
С������ÿ��ÿ������ˮ����5m3-35m3֮�䣬��7���������ˮ�۸�����Ƿ�������ν�����ÿ�����ˮ��ʽ�ĸı�. ����С�����Ƶ�ͼ���ͷ��ֵ���Ϣ������������⣺
��1��n =________��С��������_____��������ȫͼ1��
��2��ÿ��ÿ����ˮ������λ������______֮�䣬��������_______֮�䣻
��3�����С�����ڵ�С����1200����������������ӵ����Ƿ���ȡ��Ӧ����ˮ��ʽ�ı����ľ������ж��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=a��x+2��2+m��ԭ�㣬��������y2=![]() ��x��3��2+n���ڵ�A��1��3��������A��x���ƽ���ߣ��ֱ������������ڵ�B��C�����н��ۣ������������ߵĶԳ������Ϊ5����x=0ʱ��y2=5������x��3ʱ��y1��y2��0����y�����߶�BC���д��ߣ���ȷ������________����д��ȷ���۵���ţ���
��x��3��2+n���ڵ�A��1��3��������A��x���ƽ���ߣ��ֱ������������ڵ�B��C�����н��ۣ������������ߵĶԳ������Ϊ5����x=0ʱ��y2=5������x��3ʱ��y1��y2��0����y�����߶�BC���д��ߣ���ȷ������________����д��ȷ���۵���ţ���
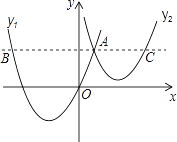
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У���E��BC�ϣ�AE��AD��DF��AE������ΪF
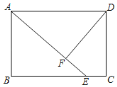
��1����֤��DF��AB��
��2������FAD��30������AB��4����AD��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com