
【题目】如图,四边形 ABCD 为正方形,取 AB 中点O ,以 AB 为直径, O 圆心作圆.
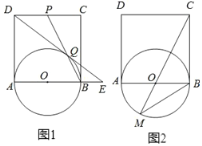
(1)如图 1,取CD 的中点 P ,连接 BP 交⊙ O 于Q ,连接 DQ 并延长交 AB 的延长线于 E ,求证: QE ![]() BE AE ;
BE AE ;
(2)如图 2,连接 CO 并延长交⊙ O 于 M 点,求tanM 的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接AQ,AP,根据直角所对的圆周角是直角可得∠AQB=∠AQP=90°,从而证出A、Q、P、D四点共圆,再根据圆周角定理的推论可得∠DAP=∠DQP,利用SAS证出△ADP≌△BCP,推出∠EBQ=∠EQA,即可证出△EBQ∽△EQA,列出比例式变形即可证出结论;
(2)延长OA至N,使ON=OC,连接CN,根据等边对等角可得∠N=∠OCN,然后根据三角形外角的性质即可推出∠M=∠N,设OB=a,则BC=2a,利用勾股定理求出OC,从而求出ON,然后求出tanN即可得出结论.
解:(1)连接AQ,AP,
∵AB 为直径
∴∠AQB=∠AQP=90°
∵四边形 ABCD 为正方形,
∴∠ADC=90°,AB∥CD,∠ADP=∠BCP=90°,AD=BC
∴∠ADC+∠AQP=180°,∠EBQ=∠DPQ
∴A、Q、P、D四点共圆
∴∠DAP=∠DQP
∴∠EQA =∠EQB+∠BQA=∠DQP+90°=∠DAP+90°=∠DAP+∠ADP=∠APC
∵DP=CP,∠ADP=∠BCP=90°,AD=BC
∴△ADP≌△BCP
∴∠APD=∠BPC
∴∠APD+∠APB=∠BPC+∠APB
∴∠DPQ=∠APC
∴∠EBQ=∠EQA
∵∠E=∠E
∴△EBQ∽△EQA
∴![]()
∴QE![]() BE AE ;
BE AE ;
(2)延长OA至N,使ON=OC,连接CN

∴∠N=∠OCN
∴∠COB=∠N+∠OCN=2∠ONC
∵OB=OM
∴∠M=∠OBM
∴∠COB=∠M+∠OBM=2∠M
∴∠M=∠N
∵四边形 ABCD 为正方形,点O为AB的中点
∴BC=AB=2OB
设OB=a,则BC=2a
根据勾股定理可得OC=![]()
∴ON=OC=![]()
∴BN=ON+OB=![]()
∴tanN=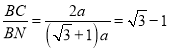
∴tanM=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,过程如下,请补充完整.
(1)收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(2)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x 人数 班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=______,n=______.
(3)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 72 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=______,y=______.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有______人.
③现从甲班指定的2名学生(1男1女),乙班指定的3名学生(2男1女)中分别抽取1名学生去参加上级部门组织的身体素质测试,用树状图和列表法求抽到的2名同学是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
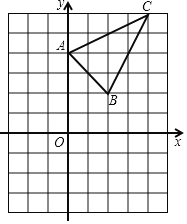
【题目】如图,△ABC在坐标平面内,三个顶点的坐标分别为A(0,4),B(2,2),C(4,6)(正方形网格中,每个小正方形的边长为1)
(1)画出△ABC向下平移5个单位得到的△A1B1C1,并写出点B1的坐标;
(2)以点O为位似中心,在第三象限画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为1:2,直接写出点C2的坐标和△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某省对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,![]() 级:对学习很感兴趣;
级:对学习很感兴趣;![]() 级:对学习较感兴趣;
级:对学习较感兴趣;![]() 级:对学习不感兴趣),并将调查结果绘制成图①和图②不完整的统计图.请根据图中提供的信息,解答下列问题:
级:对学习不感兴趣),并将调查结果绘制成图①和图②不完整的统计图.请根据图中提供的信息,解答下列问题:
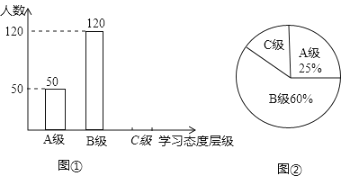
(1)此次抽样调查中,共调查了______名学生;
(2)将图①补充完整;
(3)求出图②中![]() 级所占的圆心角的度数;
级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该省近40000名八年级学生中大约有多少名学生学习态度达标(达标包括![]() 级和
级和![]() 级)?
级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ABCD 为矩形,点 E 为 BC 上的一点,满足 AB CF BE CE ,连接 DE ,延长 EF交 AD 于 M 点,若 AE ![]() FD
FD ![]() AF
AF ![]() , DEF 15°,则M 的度数为_____.
, DEF 15°,则M 的度数为_____.
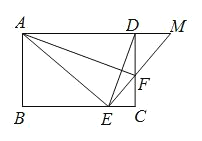
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部门对![]() ,
,![]() ,
,![]() ,
,![]() 四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出
四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出![]() 厂家的合格率为
厂家的合格率为![]() ,并根据检测数据绘制了两幅不完整的统计图.
,并根据检测数据绘制了两幅不完整的统计图.
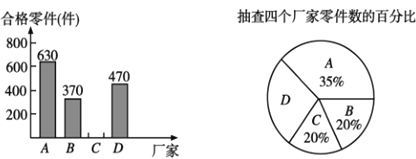
(1)抽查![]() 厂家的零件为______件,扇形统计图中
厂家的零件为______件,扇形统计图中![]() 厂家对应的圆心角为______.
厂家对应的圆心角为______.
(2)抽查![]() 厂家的合格零件为_______件.
厂家的合格零件为_______件.
(3)若要从![]() ,
,![]() ,
,![]() ,
,![]() 四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用列表法或画树状图的方法求出
四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用列表法或画树状图的方法求出![]() ,
,![]() 两个厂家同时被选中的概率,并列出所有等可能的结果.
两个厂家同时被选中的概率,并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y![]() x2沿x轴正方向平移后经过点A(x1,y2),B(x2,y2),其中x1,x2是方程x2﹣2x=0的两根,且x1>x2,
x2沿x轴正方向平移后经过点A(x1,y2),B(x2,y2),其中x1,x2是方程x2﹣2x=0的两根,且x1>x2,
(1)如图.求A,B两点的坐标及平移后抛物线的解析式;
(2)平移直线AB交抛物线于M,交x轴于N,且![]() ,求△MNO的面积;
,求△MNO的面积;
(3)如图,点C为抛物线对称轴上顶点下方的一点,过点C作直线交抛物线于E、F,交x轴于点D,探究![]() 的值是否为定值?如果是,求出其值;如果不是,请说明理由.
的值是否为定值?如果是,求出其值;如果不是,请说明理由.
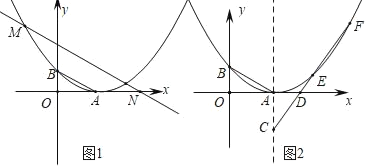
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是线段OB、OC上的动点
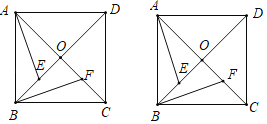
(1)如果动点E、F满足BE=OF(如图),且AE⊥BF时,问点E在什么位置?并证明你的结论;
(2)如果动点E、F满足BE=CF(如图),写出所有以点E或F为顶点的全等三角形(不得添加辅助线).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com