
���� ��1��������ʾ��x��y�ú�a��ʽ�Ӵ��棬���ɣ�
��2����3.456=a����a��ʾʽ���е�����Ȼ���ٴ�����ֵ���㼴�ɣ�
��3����$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$=a��$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$=b��Ȼ����������ʽ�ӽ��л��ɣ�
��� �⣺��1����x-y=��a+1����a-2��-a��a-1��=a2-a-2-a2+a=-2��0��
��x��y��
�ʴ��ǣ�-2��0������
��2����3.456=a��
��ԭʽ=a��a-1����a+2��-a3-��a-2��2
=2a-4
=2.912��
��3����$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$=a��$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$=b��
ԭʽ=��1-a��b-��1-b��a=b-a=$\frac{1}{6}$��
���� ���⿼����ʽ�Ļ�����㣬��ȷ������֪�е���ʾ�����Ԫ�Ľ���˼·�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
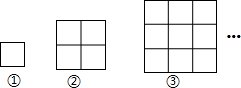 ��ͼ��ÿһ��ͼ�о��������ɸ������Σ��ڢٸ�ͼ���к���1�������Σ��ڢڸ�ͼ���к���5�������Σ����˹�����ȥ����ڢ�ͼ���������εĸ����ǣ�������
��ͼ��ÿһ��ͼ�о��������ɸ������Σ��ڢٸ�ͼ���к���1�������Σ��ڢڸ�ͼ���к���5�������Σ����˹�����ȥ����ڢ�ͼ���������εĸ����ǣ�������| A�� | 102 | B�� | 91 | C�� | 55 | D�� | 31 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 6 | C�� | -6 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com