
分析 ①若-a>b>0,则a<0,b>0,所以ab<0,据此判断即可.
②若ab>0,则a>0,b>0或a<0,b<0,据此判断即可.
③若a>b,c≠0,则c>0时,ac>bc;c<0时,ac<bc;据此判断即可.
④若a>b,c≠0,则c2>0,所以ac2>bc2,据此判断即可.
⑤若a>b,c≠0,则-a<-b,所以-a-c<-b-c,据此解答即可.
解答 解:∵-a>b>0,
∴a<0,b>0,
∴ab<0,①正确;
∵ab>0,
∴a>0,b>0或a<0,b<0,②错误;
∵a>b,c≠0,
∴c>0时,ac>bc;c<0时,ac<bc;③错误;
∵a>b,c≠0,
∴c2>0,
∴ac2>bc2,④正确;
∵a>b,c≠0,
∴-a<-b,
∴-a-c<-b-c,⑤正确.
综上,可得
判断中,正确的序号为:①④⑤.
故答案为:①④⑤.
点评 此题主要考查了不等式的基本性质:(1)不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;(2)不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;(3)不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
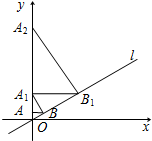 如图,已知直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A5的坐标为(0,210).
如图,已知直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A5的坐标为(0,210).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
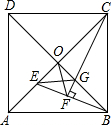 如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO于E点,CF⊥BE于F点,交BO于G点,连接EG、OF.下列三个结论:①CE=CB;②AE=$\sqrt{2}$OE;③OF=$\frac{1}{2}$CG.其中正确的结论只有( )
如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO于E点,CF⊥BE于F点,交BO于G点,连接EG、OF.下列三个结论:①CE=CB;②AE=$\sqrt{2}$OE;③OF=$\frac{1}{2}$CG.其中正确的结论只有( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c=$\frac{a}{sinA}$ | B. | c=$\frac{a}{cosA}$ | C. | c=a•tanA | D. | c=$\frac{a}{tanA}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a+b)2=4a2+b2 | B. | ${({2^{-2}}-\frac{1}{4})^0}=1$ | C. | -2x6÷x2=-2x3 | D. | (x-y)3(y-x)2=(x-y)5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com