
【题目】如图,在平面直角坐标系中,点B在函数y=x图象上,点A在x轴的正半轴上,等腰直角三角形BCD的顶点C在AB上,点D在函数y=![]() 第一象限的图象上若△OAB与△BCD面积的差为2,则k的值为( )
第一象限的图象上若△OAB与△BCD面积的差为2,则k的值为( )
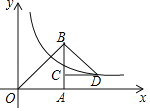
A.8B.4C.2D.1
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
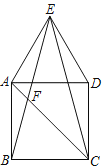
【题目】如图,在正方形ABCD的上方作等边三角形ADE,连接BE,CE.
(1)求证:△ABE≌△DCE;
(2)连接AC,设AC与BE交于点F,求∠BFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么sin∠BED的值为( )
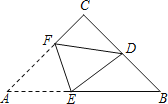
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中,直线l与x、y轴分别交于点A(4,0)、B(0,![]() )两点,∠BAO的角平分线交y轴于点D. 点C为直线l上一点,以AC为直径的⊙G经过点D,且与x轴交于另一点E.
)两点,∠BAO的角平分线交y轴于点D. 点C为直线l上一点,以AC为直径的⊙G经过点D,且与x轴交于另一点E.
(1)求证:y轴是⊙G的切线;
(2)求出⊙G的半径r,并直接写出点C的坐标;
(3)如图2,若点F为⊙G上的一点,连接AF,且满足∠FEA=45°,请求出EF的长?
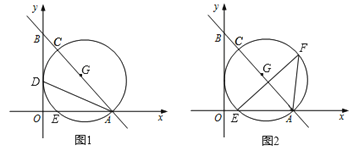
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(2m﹣1)x﹣2m(m>0.5)的最低点的纵坐标为﹣4.

(1)求抛物线的解析式;
(2)如图1,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,D为抛物线上的一点,BD平分四边形ABCD的面积,求点D的坐标;
(3)如图2,平移抛物线y=x2+(2m﹣1)x﹣2m,使其顶点为坐标原点,直线y=﹣2上有一动点P,过点P作两条直线,分别与抛物线有唯一的公共点E、F(直线PE、PF不与y轴平行),求证:直线EF恒过某一定点.
查看答案和解析>>
科目:初中数学 来源: 题型:
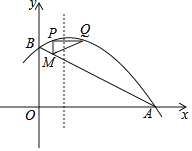
【题目】如图,在平面直角坐标系中,抛物线y=ax2+![]() x+2与x轴交于点A(4,0)与y轴交于点B.点M在线段AB上,其横坐标为m,PM∥y轴,与抛物线交点为点P,PQ∥x轴,与抛物线交点为点Q
x+2与x轴交于点A(4,0)与y轴交于点B.点M在线段AB上,其横坐标为m,PM∥y轴,与抛物线交点为点P,PQ∥x轴,与抛物线交点为点Q
(1)求a的值、并写出此抛物线顶点的坐标;
(2)求m为何值时,△PMQ为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为4,点O是△ABC的外心,∠FOG=120°.绕点O旋转∠FOG,分别交线段AB、BC于D、E两点.连接DE给出下列四个结论:①OD=OE;②S△ODE=S△BDE;③S四边形ODBE=![]() ;④△BDE周长的最小值为6.上述结论中正确的个数是( )
;④△BDE周长的最小值为6.上述结论中正确的个数是( )
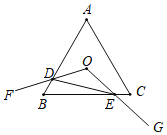
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽台州”,我市某社区将辖区内一块不超过1000平方米的区域进行美化.经调查,美化面积为100平方米时,每平方米的费用为300元.每增加1平方米,每平方米的费用下降0.2元。设美化面积增加x平方米,美化所需总费用为y元.
(1)求y与x的函数关系式;
(2)当美化面积增加100平方米时,美化的总费用为多少元;
(3)当美化面积增加多少平方米时,美化所需费用最高?最高费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤![]() .
.
你认为其中正确信息的个数有

A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com