

分析 (1)通过延长BA交EF于一点M,则∠CAD=180°-∠BAC-∠EAM即可求得;
(2)作AH⊥CD于H点,作CG⊥AE于G点,先求得CD的长,然后再求得CG的长.
解答 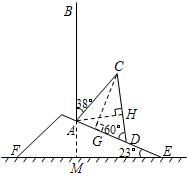 解:(1)延长BA交EF于点M.
解:(1)延长BA交EF于点M.
在Rt△AME中,∠E=23°,
∴∠MAE=67°.
又∵∠BAC=38°,
∴∠DAC=180°-67°-38°=75°;
(2)作AH⊥CD于H点,作CG⊥AE于G点.
在△ADH中,∠ADC=60°,AD=4,cos∠ADC=$\frac{DH}{AD}$,
∴DH=2.
sin∠ADC=$\frac{AH}{AD}$,
∴AH=2$\sqrt{3}$.
在Rt△ACH中,∠C=180°-75°-60°=45°,
∴CH=AH=2$\sqrt{3}$.
∴CD=DH+CH=2$\sqrt{3}$.
在Rt△CDG中,∠CDG=60°,sin∠CDG=$\frac{CG}{CD}$,∴CG=3+$\sqrt{3}$≈5米.
答:折点C距离坡面AE约为5米.
点评 本题主要考查学生对坡度坡角的掌握及三角函数的运用能力,但综合性较强,有一定的复杂性.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
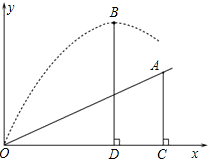 如图,小明在一次高尔夫球赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线.如果不考虑空气阻力,当球打到最大竖直高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30°,O、A两点相距$\frac{12}{5}$米.在如图所建立的平面直角坐标系下
如图,小明在一次高尔夫球赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线.如果不考虑空气阻力,当球打到最大竖直高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30°,O、A两点相距$\frac{12}{5}$米.在如图所建立的平面直角坐标系下查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
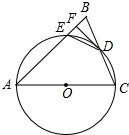 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲成绩 | 9 | 4 | 7 | 4 | 6 |
| 乙成绩 | 7 | 5 | 7 | a | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com