
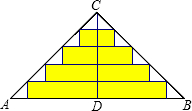
 如图,△ABC是一张直角三角形彩色纸,AC=15cm,BC=20cm.若将斜边上的高CD 分成n等分,然后裁出(n-1)张宽度相等的长方形纸条.则这(n-1)张纸条的面积和是$\frac{150(n-1)}{n}$cm2.
如图,△ABC是一张直角三角形彩色纸,AC=15cm,BC=20cm.若将斜边上的高CD 分成n等分,然后裁出(n-1)张宽度相等的长方形纸条.则这(n-1)张纸条的面积和是$\frac{150(n-1)}{n}$cm2. 分析 先利用勾股定理计算出AB=25,再利用面积法计算出CD=12,接着证明△CEF∽△CAB,则可计算出EF=$\frac{1}{n}$•25,同理可得从上往下数,第2个矩形的长为$\frac{2}{n}$•25,…,从上往下数,第(n-1)个矩形的长为$\frac{n-1}{n}$•25,且所有矩形的宽的和为$\frac{1}{n}$•12,然后把所有矩形的面积相加即可.
解答 解:如图,∵∠ACB=90°,AC=15,BC=20,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=25,
∵$\frac{1}{2}$CD•AB=$\frac{1}{2}$AC•BC,
∴CD=12,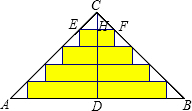 ∵斜边上的高CD分成n等分,
∵斜边上的高CD分成n等分,
∴CH=$\frac{12}{n}$,
∵EF∥AB,
∴△CEF∽△CAB,
∴$\frac{EF}{AB}$=$\frac{CH}{CD}$,即$\frac{EF}{25}$=$\frac{1}{n}$,解得EF=$\frac{1}{n}$•25,
即从上往下数,第1个矩形的长为$\frac{1}{n}$•25,
同理可得从上往下数,第2个矩形的长为$\frac{2}{n}$•25,
…
从上往下数,第(n-1)个矩形的长为$\frac{n-1}{n}$•25,
而所有矩形的宽都为$\frac{1}{n}$•12,
∴这(n-1)张纸条的面积和是=[$\frac{1}{n}$•25+$\frac{2}{n}$•25+…+$\frac{n-1}{n}$•25]•$\frac{1}{n}$•12
=$\frac{25}{n}$(1+2+…+n-1)•$\frac{1}{n}$•12
=$\frac{150(n-1)}{n}$(cm2).
故答案为$\frac{150(n-1)}{n}$.
点评 本题考查了相似三角形的应用:从实际问题中抽象出几何图形,然后利用相似三角形的性质求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
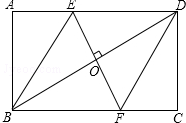 如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为3$\sqrt{3}$.
如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源:2017届福建省仙游县郊尾、枫亭五校教研小片区九年级下学期第一次月考数学试卷(解析版) 题型:解答题
抛物线经过A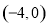 ,B
,B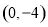 ,C
,C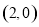 三点.
三点.
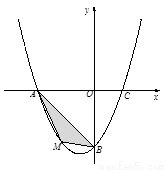
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线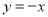 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50名学生 | B. | 50名学生的身高 | C. | 400名学生 | D. | 400名学生的身高 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
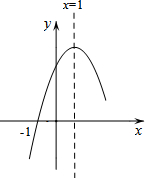 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(-1,0).则下面的四个结论:①2a+b=0;②8a+c<0;③abc>0;④当y<0时,x<-1或x>2,⑤对任意实数m,m(am+b)≤a+b.其中正确的结论有( )个.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(-1,0).则下面的四个结论:①2a+b=0;②8a+c<0;③abc>0;④当y<0时,x<-1或x>2,⑤对任意实数m,m(am+b)≤a+b.其中正确的结论有( )个.| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com