
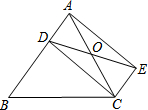
 如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.
如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.  亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 99200 | B. | 992×102 | C. | 9.92×106 | D. | 9.92×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
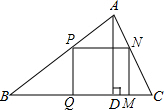 如图,△ABC是一块锐角三角形的余料,它的边BC=120mm,高AD=80mm.要把它加工成一个矩形零件PQMN,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,问要使加工成的这个矩形面积最大,那么边长MN应是多少mm?
如图,△ABC是一块锐角三角形的余料,它的边BC=120mm,高AD=80mm.要把它加工成一个矩形零件PQMN,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,问要使加工成的这个矩形面积最大,那么边长MN应是多少mm?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com