
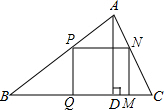
 如图,△ABC是一块锐角三角形的余料,它的边BC=120mm,高AD=80mm.要把它加工成一个矩形零件PQMN,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,问要使加工成的这个矩形面积最大,那么边长MN应是多少mm?
如图,△ABC是一块锐角三角形的余料,它的边BC=120mm,高AD=80mm.要把它加工成一个矩形零件PQMN,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,问要使加工成的这个矩形面积最大,那么边长MN应是多少mm? 分析 PN与AD交于点E,如图,设MN=xmm,则AE=AD-ED=80-x,再证明△APN∽△ABC,利用相似比可表示出PN=$\frac{3}{2}$(80-x),根据矩形的面积公式得到S矩形PQMN=PN•MN=$\frac{3}{2}$(80-x)•x,接着配方得到S矩形PQMN=-$\frac{3}{2}$(x-40)2+2400,然后根据二次函数的最值问题求解.
解答 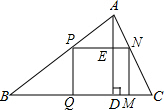 解:PN与AD交于点E,如图,设MN=xmm,
解:PN与AD交于点E,如图,设MN=xmm,
易得四边形MNED为矩形,则ED=MN=x,
∴AE=AD-ED=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴$\frac{PN}{BC}$=$\frac{AE}{AD}$,即$\frac{PN}{120}$=$\frac{80-x}{80}$,
∴PN=$\frac{3}{2}$(80-x),
∴S矩形PQMN=PN•MN=$\frac{3}{2}$(80-x)•x=-$\frac{3}{2}$(x-40)2+2400,
当x=40时,S矩形PQMN,有最大值,最大值为2400(mm2).
答:要使加工成的这个矩形面积最大,那么边长MN应是40mm.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.也考查了二次函数的最值问题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-$\frac{1}{2}$(x+1)2+1 | B. | y=-$\frac{1}{2}$(x+1)2-1 | C. | y=-$\frac{1}{2}$(x-1)2+1 | D. | y=-$\frac{1}{2}$(x-1)2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对玉坎河水质情况的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对某班50名同学体重情况的调查 | |
| D. | 对为某类烟花爆竹燃放安全情况的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com