
ЁОЬтФПЁПФГЪ§бЇаЁзщдкЪ§бЇПЮЭтЛюЖЏжаЃЌбаОПШ§НЧаЮКЭе§ЗНаЮЕФаджЪЪБЃЌзіСЫШчЯТЬНОПЃК
дкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃЌЕуDЮЊжБЯпBCЩЯвЛЖЏЕу(ЕуDВЛгыBЃЌCжиКЯ)ЃЌ
вдADЮЊБпдкADгвВрзїе§ЗНаЮADEFЃЌСЌНгCFЃЎ
(1).ШчЭМ1ЃЌЕБЕуDдкЯпЖЮBCЩЯЪБЃЌ
Ђй.BCгыCFЕФЮЛжУЙиЯЕЮЊЃК________________________________ЃЎ
Ђк.BCЃЌCDЃЌCFжЎМфЕФЪ§СПЙиЯЕЮЊЃК_______________________________.
(2).ШчЭМ2ЃЌЕБЕуDдкЯпЖЮCBЕФбгГЄЯпЩЯЪБЃЌНсТлЂйЃЌЂкЪЧЗёШдШЛГЩСЂЃПШєГЩСЂЃЌ
ЧыИјгшжЄУїЃЛШєВЛГЩСЂЃЌЧыФуаДГіе§ШЗНсТлдйИјгшжЄУїЃЎ
(3).ШчЭМ3ЃЌНЋЭМ2жаЕФ ABЃНACИФБфГЩABЃНkACЃЌе§ЗНаЮADEFИФГЩОиаЮADEFЃЌЧвAD=kAF,ЦфЫќЬѕМўВЛБф ЃЌВТЯыЯпЖЮBDгыCFжЎМфЕФЙиЯЕЃЌЫЕУїРэгЩ.


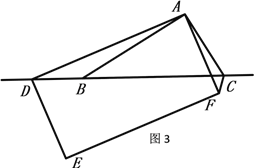
ЁОД№АИЁП(1) ЂйBCгыCFЕФЮЛжУЙиЯЕЮЊЃКBCЁЭCF ЃЛЂкBCЃЌCDЃЌCFжЎМфЕФЪ§СПЙиЯЕЮЊЃКBC=CF+CDЃЌжЄУїМћНтЮіЃЛ(2)НсТлЂйГЩСЂЃЌЂкВЛГЩСЂЃЌBCЃЌCDЃЌCFжЎМфЕФЪ§СПЙиЯЕЮЊBC=CD-CFЛђCD=BC+CFЃЌжЄУїМћНтЮіЃЛ(3).Ъ§СПЙиЯЕBD=kCFЃЌЮЛжУЙиЯЕBCЁЭCFЃЌжЄУїМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУе§ЗНаЮБпЯрЕШЃЌЕШбќШ§НЧаЮЃЌжЄУї![]() ABD КЭ
ABD КЭ ![]() AFCШЋЕШЃЌдйжЄУїЁЯFCB=90ЁуЃЛ
AFCШЋЕШЃЌдйжЄУїЁЯFCB=90ЁуЃЛ
ЃЈ2ЃЉНтЬтЗНЗЈВЮПМЃЈ1ЃЉЃЛ
ЃЈ3ЃЉВЮПМЃЈ1ЃЉЬтдРэЃЌжЄУї![]() ABD КЭ
ABD КЭ ![]() AFCЯрЫЦЃЌПЩвджЄУїBD=kCFЃЌ
AFCЯрЫЦЃЌПЩвджЄУїBD=kCFЃЌ
НтЃКЃЈ1ЃЉ![]() ABЃНACЃЌAD=AF,
ABЃНACЃЌAD=AF,
![]() ЁЯBAD+ЁЯDAC=ЁЯFAC+ЁЯDAC,
ЁЯBAD+ЁЯDAC=ЁЯFAC+ЁЯDAC,
![]() ЁЯBAD=ЁЯCAF,
ЁЯBAD=ЁЯCAF,
![]() ABD
ABD![]()
![]() AFCЃЌ
AFCЃЌ
![]() ЁЯABD=ЁЯACF.
ЁЯABD=ЁЯACF.
![]() .
.
![]() BCЁЭCF
BCЁЭCF
![]() C=BC+CF.
C=BC+CF.
ЃЈ2ЃЉ![]() ABЃНACЃЌAD=AF,
ABЃНACЃЌAD=AF,
![]() ЁЯBAD+ЁЯDAC=ЁЯFAC+ЁЯDAC,
ЁЯBAD+ЁЯDAC=ЁЯFAC+ЁЯDAC,
![]() ЁЯBAD=ЁЯCAF,
ЁЯBAD=ЁЯCAF,
![]() ABD
ABD![]()
![]() AFCЃЌ
AFCЃЌ
![]() ЁЯADB=ЁЯAFC.
ЁЯADB=ЁЯAFC.
![]() . BCЁЭCF
. BCЁЭCF
НсТлЂйГЩСЂЃЌЂкВЛГЩСЂЃЌ
![]() CD=BC+CF.
CD=BC+CF.
ЃЈ3ЃЉ![]() ABЃНkACЃЌAD=kAF,
ABЃНkACЃЌAD=kAF,
![]() ЁЯBAD+ЁЯDAC=ЁЯFAC+ЁЯDAC,
ЁЯBAD+ЁЯDAC=ЁЯFAC+ЁЯDAC,
![]() ЁЯBAD=ЁЯCAF,
ЁЯBAD=ЁЯCAF,
![]() ABD
ABD![]()
![]() AFCЃЌ
AFCЃЌ
![]() BD=kCF.
BD=kCF.
![]() ЁЯADB=ЁЯAFC.
ЁЯADB=ЁЯAFC.
![]() .
.
BCЁЭCF.


 ОЋгЂПкЫуПЈЯЕСаД№АИ
ОЋгЂПкЫуПЈЯЕСаД№АИ гІгУЬтЕуВІЯЕСаД№АИ
гІгУЬтЕуВІЯЕСаД№АИ зДдЊМАЕкЯЕСаД№АИ
зДдЊМАЕкЯЕСаД№АИ ЭЌВНАТЪ§ЯЕСаД№АИ
ЭЌВНАТЪ§ЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
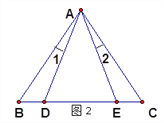
ЁОЬтФПЁПШчЭМЃЌдкЕШБпЁїABCжаЃЌDЮЊBCБпЩЯвЛЕуЃЌEЮЊACБпЩЯвЛЕуЃЌЧвЁЯADB+ЁЯEDC=120ЁуЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABDЁзЁїDCEЃЛ
ЃЈ2ЃЉШєCD=12ЃЌCE=3ЃЌЧѓЁїABCЕФжмГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
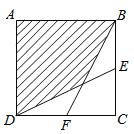
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ4cmЃЌЕуEЃЌFЗжБ№ЪЧBCЃЌCDЕФжаЕуЃЌСЌНсBFЃЌDEЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЪЧ________cm2.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁЯФЭЌбЇДгМвЕНбЇаЃга![]() ЃЌ
ЃЌ![]() СНЬѕВЛЭЌЕФЙЋНЛЯпТЗЃЎЮЊСЫНтдчИпЗхЦкМфетШ§ЬѕЯпТЗЩЯЕФЙЋНЛГЕДгМзЕиЕНввЕиЕФгУЪБЧщПіЃЌдкУПЬѕЯпТЗЩЯЫцЛњбЁШЁСЫ500ИіАрДЮЕФЙЋНЛГЕЃЌЪеМЏСЫетаЉАрДЮЕФЙЋНЛГЕгУЪБЃЈЕЅЮЛЃКЗжжгЃЉЕФЪ§ОнЃЌЭГМЦШчЯТЃК
СНЬѕВЛЭЌЕФЙЋНЛЯпТЗЃЎЮЊСЫНтдчИпЗхЦкМфетШ§ЬѕЯпТЗЩЯЕФЙЋНЛГЕДгМзЕиЕНввЕиЕФгУЪБЧщПіЃЌдкУПЬѕЯпТЗЩЯЫцЛњбЁШЁСЫ500ИіАрДЮЕФЙЋНЛГЕЃЌЪеМЏСЫетаЉАрДЮЕФЙЋНЛГЕгУЪБЃЈЕЅЮЛЃКЗжжгЃЉЕФЪ§ОнЃЌЭГМЦШчЯТЃК
ЙЋНЛГЕгУЪБ ЦЕЪ§ ЙЋНЛГЕТЗЯп |
|
|
|
| змМЦ |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
ОнДЫЙРМЦЃЌдчИпЗхЦкМфЃЌГЫзј![]() ЯпТЗЁАгУЪБВЛГЌЙ§35ЗжжгЁБЕФИХТЪЮЊ__________ЃЌШєвЊдк40ЗжжгжЎФкЕНДябЇаЃЃЌгІОЁСПбЁдёГЫзј__________ЃЈЬю
ЯпТЗЁАгУЪБВЛГЌЙ§35ЗжжгЁБЕФИХТЪЮЊ__________ЃЌШєвЊдк40ЗжжгжЎФкЕНДябЇаЃЃЌгІОЁСПбЁдёГЫзј__________ЃЈЬю![]() Лђ
Лђ![]() ЃЉЯпТЗЃЎ
ЃЉЯпТЗЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃН6ЃЌACЃН8ЃЌBCЃН10ЃЌPЮЊБпBCЩЯвЛЖЏЕуЃЈЧвЕуPВЛгыЕуBЁЂCжиКЯЃЉЃЌPEЁЭABгкEЃЌPFЁЭACгкFЃЌMЮЊEFжаЕуЃЎЩшAMЕФГЄЮЊxЃЌдђxЕФШЁжЕЗЖЮЇЪЧ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
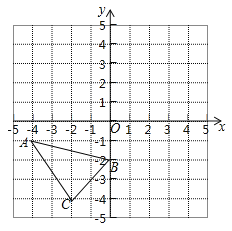
ЁОЬтФПЁПШчЭМЃЌЁїABCЕФШ§ИіЖЅЕуЖМдкБпГЄЮЊ1ЕФаЁе§ЗНаЮзщГЩЕФЭјИёЕФИёЕуЩЯЃЌвдЕуOЮЊдЕуНЈСЂжБНЧзјБъЯЕЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉНЋЁїABCЯШЯђЩЯЦНвЦ5ИіЕЅЮЛЃЌдйЯђгвЦНвЦ1ИіЕЅЮЛЕУЕНЁїA1B1C1ЃЌЛГіЁїA1B1C1ЃЌВЂжБНгаДГіA1ЕФзјБъЁЁ ЁЁЃЛ
ЃЈ2ЃЉНЋЁїA1B1C1ШЦЕуЃЈ0ЃЌЉ1ЃЉЫГЪБеыа§зЊ90ЁуЕУЕНЁїA2B2C2ЃЌЛГіA2B2C2ЃЛ
ЃЈ3ЃЉЙлВьЭМаЮЗЂЯжЃЌA2B2C2ЪЧгЩЁїABCШЦЕуЁЁ ЁЁЫГЪБеыа§зЊЁЁ ЁЁЖШЕУЕНЕФЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗДБШР§КЏЪ§yЃН![]() гыyЃН
гыyЃН![]() ЕФЭМЯѓЩЯЗжБ№гавЛЕуAЃЌBЃЌЧвABЁЮxжсЃЌADЁЭxжсгкDЃЌBCЁЭxжсгкCЃЌШєОиаЮABCDЕФУцЛ§ЮЊ8ЃЌдђbЉaЃНЃЈЁЁЁЁЃЉ
ЕФЭМЯѓЩЯЗжБ№гавЛЕуAЃЌBЃЌЧвABЁЮxжсЃЌADЁЭxжсгкDЃЌBCЁЭxжсгкCЃЌШєОиаЮABCDЕФУцЛ§ЮЊ8ЃЌдђbЉaЃНЃЈЁЁЁЁЃЉ
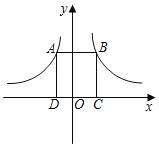
A.8B.Љ8C.4D.Љ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцФкШнЃЌВЂАДвЊЧѓНтОіЮЪЬтЃК
ЮЪЬтЃКЁАдкЦНУцФкЃЌвбжЊЗжБ№га2ИіЕуЃЌ3ИіЕуЃЌ4ИіЕуЃЌ5ИіЕуЃЌЁЃЌ![]() ИіЕуЃЌЦфжаШЮвтШ§ИіЕуЖМВЛдкЭЌвЛЬѕжБЯпЩЯОЙ§УПСНЕуЛвЛЬѕжБЯпЃЌЫќУЧПЩвдЗжБ№ЛЖрЩйЬѕжБЯпЃПЁБ
ИіЕуЃЌЦфжаШЮвтШ§ИіЕуЖМВЛдкЭЌвЛЬѕжБЯпЩЯОЙ§УПСНЕуЛвЛЬѕжБЯпЃЌЫќУЧПЩвдЗжБ№ЛЖрЩйЬѕжБЯпЃПЁБ
ЬНОПЃКЮЊСЫНтОіетИіЮЪЬтЃЌЯЃЭћаЁзщЕФЭЌбЇУЧЃЌЩшМЦСЫШчЯТБэИёНјааЬНОПЃКЃЈЮЊСЫЗНБубаОПЮЪЬтЃЌЭМжаУПЬѕЯпЖЮБэЪОЙ§ЯпЖЮСНЖЫЕуЕФвЛЬѕжБЯпЃЉ
ЕуЪ§ | 2 | 3 | 4 | 5 | Ё |
|
ЪОвтЭМ |
|
|
|
| Ё |
|
жБЯпЬѕЪ§ | 1 |
|
|
| Ё |
ЧыНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧыАяжњЯЃЭћаЁзщЙщФЩЃЌВЂжБНгаДГіНсТлЃКЕБЦНУцФкгаИіЕуЪБЃЌжБЯпЬѕЪ§ЮЊ______ЃЛ
ЃЈ2ЃЉШєФГЭЌбЇАДееБОЬтжаЕФЗНЗЈЃЌЙВЛСЫ28ЬѕжБЯпЃЌЧѓИУЦНУцФкгаЖрЩйИівбжЊЕуЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіШчЯТЖЈвхЃКЖдгкЁбOЕФЯвMNКЭЁбOЭтвЛЕуPЃЈMЃЌOЃЌNШ§ЕуВЛЙВЯпЃЌЧвЕуPЃЌOдкжБЯпMNЕФвьВрЃЉЃЌЕБЁЯMPN+ЁЯMONЃН180ЁуЪБЃЌдђГЦЕуPЪЧЯпЖЮMNЙигкЕуOЕФЙиСЊЕуЃЎЭМ1ЪЧЕуPЮЊЯпЖЮMNЙигкЕуOЕФЙиСЊЕуЕФЪОвтЭМЃЎ

дкЦНУцжБНЧзјБъЯЕxOyжаЃЌЁбOЕФАыОЖЮЊ1ЃЎ
ЃЈ1ЃЉШчЭМ2ЃЌвбжЊMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌNЃЈ
ЃЉЃЌNЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌдкAЃЈ1ЃЌ0ЃЉЃЌBЃЈ1ЃЌ1ЃЉЃЌCЃЈ
ЃЉЃЌдкAЃЈ1ЃЌ0ЃЉЃЌBЃЈ1ЃЌ1ЃЉЃЌCЃЈ![]() ЃЌ0ЃЉШ§ЕужаЃЌЪЧЯпЖЮMNЙигкЕуOЕФЙиСЊЕуЕФЪЧЁЁ ЁЁЃЛ
ЃЌ0ЃЉШ§ЕужаЃЌЪЧЯпЖЮMNЙигкЕуOЕФЙиСЊЕуЕФЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌMЃЈ0ЃЌ1ЃЉЃЌNЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌЕуDЪЧЯпЖЮMNЙигкЕуOЕФЙиСЊЕуЃЎ
ЃЉЃЌЕуDЪЧЯпЖЮMNЙигкЕуOЕФЙиСЊЕуЃЎ
ЂйЁЯMDNЕФДѓаЁЮЊЁЁ ЁЁЃЛ
ЂкдкЕквЛЯѓЯоФкгавЛЕуEЃЈ![]() mЃЌmЃЉЃЌЕуEЪЧЯпЖЮMNЙигкЕуOЕФЙиСЊЕуЃЌХаЖЯЁїMNEЕФаЮзДЃЌВЂжБНгаДГіЕуEЕФзјБъЃЛ
mЃЌmЃЉЃЌЕуEЪЧЯпЖЮMNЙигкЕуOЕФЙиСЊЕуЃЌХаЖЯЁїMNEЕФаЮзДЃЌВЂжБНгаДГіЕуEЕФзјБъЃЛ
ЂлЕуFдкжБЯпyЃНЉ![]() x+2ЩЯЃЌЕБЁЯMFNЁнЁЯMDNЪБЃЌЧѓЕуFЕФКсзјБъxЕФШЁжЕЗЖЮЇЃЎ
x+2ЩЯЃЌЕБЁЯMFNЁнЁЯMDNЪБЃЌЧѓЕуFЕФКсзјБъxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com