
【题目】已知抛物线y=x2﹣bx+c(b,c为常数,b>0)经过点A(﹣1,0),点M(m,0)是x轴正半轴上的动点.
(1)当b=2时,求抛物线的顶点坐标;
(2)点D(b,yD)在抛物线上,当AM=AD,m=3时,求b的值;
(3)点Q(b+![]() ,yQ)在抛物线上,当
,yQ)在抛物线上,当![]() AM+2
AM+2![]() QM的最小值为
QM的最小值为![]() 时,求b的值.(说明:yD表示D点的纵坐标,yQ表示Q点的纵坐标)
时,求b的值.(说明:yD表示D点的纵坐标,yQ表示Q点的纵坐标)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)6.
;(3)6.
【解析】
(1)将点A坐标及b的值代入可得抛物线解析式,化为顶点式可得顶点坐标.
(2)将点D横坐标代入可得其纵坐标yD=﹣b﹣1,由b>0可判断其所在象限,过点D作DE⊥x轴,垂足为E,则点E(b,0),表示出AE、DE长,可知AE=DE,在Rt△ADE中,得AD=![]() AE,由AM=AD求出b值即可;
AE,由AM=AD求出b值即可;
(3)求出yQ,可知点Q(b+![]() ,﹣
,﹣![]() ﹣
﹣![]() )在第四象限,且在直线x=b的右侧,可取点N(0,1),过点Q作直线AN的垂线,垂足为G,QG与x轴相交于点M,过点Q作QH⊥x轴于点H,则点H(b+
)在第四象限,且在直线x=b的右侧,可取点N(0,1),过点Q作直线AN的垂线,垂足为G,QG与x轴相交于点M,过点Q作QH⊥x轴于点H,则点H(b+![]() ,0),在Rt△MQH中,可知∠QMH=∠MQH=45°,设点M(m,0),可用含b的代数式表示m,由
,0),在Rt△MQH中,可知∠QMH=∠MQH=45°,设点M(m,0),可用含b的代数式表示m,由![]() AM+2
AM+2![]() QM=
QM=![]() 列出方程求解即可.
列出方程求解即可.
解:(1)∵抛物线y=x2﹣bx+c经过点A(﹣1,0),
∴1+b+c=0,
即c=﹣b﹣1,
当b=2时,
y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的顶点坐标为(1,﹣4);
(2)由(1)知,抛物线的解析式为y=x2﹣bx﹣b﹣1,
∵点D(b,yD)在抛物线y=x2﹣bx﹣b﹣1上,
∴yD=b2﹣bb﹣b﹣1=﹣b﹣1,
由b>0,得b>![]() >0,﹣b﹣1<0,
>0,﹣b﹣1<0,
∴点D(b,﹣b﹣1)在第四象限,且在抛物线对称轴x=![]() 的右侧,
的右侧,
如图1,过点D作DE⊥x轴,垂足为E,则点E(b,0),

∴AE=/span>b+1,DE=b+1,得AE=DE,
∴在Rt△ADE中,∠ADE=∠DAE=45°,
∴AD=![]() AE,
AE,
由已知AM=AD,m=3,
∴3﹣(﹣1)=![]() (b+1),
(b+1),
∴b=2![]() ﹣1;
﹣1;
(3)∵点Q(b+![]() ,yQ)在抛物线y=x2﹣bx﹣b﹣1上,
,yQ)在抛物线y=x2﹣bx﹣b﹣1上,
∴yQ=(b+![]() )2﹣b(b+
)2﹣b(b+![]() )﹣b﹣1=﹣
)﹣b﹣1=﹣![]() ﹣
﹣![]() ,
,
可知点Q(b+![]() ,﹣
,﹣![]() ﹣
﹣![]() )在第四象限,且在直线x=b的右侧,
)在第四象限,且在直线x=b的右侧,
∵![]() AM+2
AM+2![]() QM=2
QM=2![]() (
(![]() AM+QM),
AM+QM),
∴可取点N(0,1),
如图2,过点Q作直线AN的垂线,垂足为G,QG与x轴相交于点M,
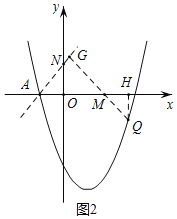
由∠GAM=45°,得![]() AM=GM,
AM=GM,
则此时点M满足题意,
过点Q作QH⊥x轴于点H,则点H(b+![]() ,0),
,0),
在Rt△MQH中,可知∠QMH=∠MQH=45°,
∴QH=MH,QM=![]() MH,
MH,
∵点M(m,0),
∴0﹣(﹣![]() ﹣
﹣![]() )=(b+
)=(b+![]() )﹣m,
)﹣m,
解得m=![]() ﹣
﹣![]() ,
,
∵![]() AM+2
AM+2![]() QM=
QM=![]() ,
,
∴![]() [(
[(![]() ﹣
﹣![]() )﹣(﹣1)]+2
)﹣(﹣1)]+2![]()
![]() [(b+
[(b+![]() )﹣(
)﹣(![]() ﹣
﹣![]() )]=
)]=![]() ,
,
∴b=6.


科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10 …,这样的数称为“三角形数”,而把1、4、9、16…,这样的数称为“正方形数”.
(1)第5个三角形数是 ,第n个“三角形数”是 ,第5个“正方形数”是 ,第n个正方形数是 ;
(2)经探究我们发现:任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.
例如:①4=1+3,②9=3+6,③16=6+10,④ ,⑤ ,….
请写出上面第4个和第5个等式;
(3)在(2)中,请探究第n个等式,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
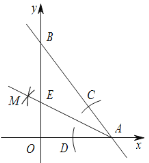
【题目】如图,直线y![]() x4与 x轴、y轴的交点为A,B.按以下步骤作图:
x4与 x轴、y轴的交点为A,B.按以下步骤作图:
①以点 A 为圆心,适当长度为半径作弧,分别交 AB,x 轴于点 C,D;
②分别以点 C,D 为圆心,大于![]() CD的长为半径作弧,两弧在∠OAB内交于点M;③作射线AM,交 y 轴于点E.则点 E 的坐标为____________
CD的长为半径作弧,两弧在∠OAB内交于点M;③作射线AM,交 y 轴于点E.则点 E 的坐标为____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆70华诞期间,各超市购物市民络绎不绝,呈现浓浓节日气氛.“百姓超市”用320元购进一批葡萄,上市后很快脱销,该超市又用680元购进第二批葡萄,所购数量是第一批购进数量的2倍,但进价每市斤多了0.2元.
(1)该超市第一批购进这种葡萄多少市斤?
(2)如果这两次购进的葡萄售价相同,且全部售完后总利润不低于![]() ,那么每市斤葡萄的售价应该至少定为多少元?
,那么每市斤葡萄的售价应该至少定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,b,定义新运算“*”:a*b=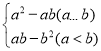 ,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.
,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.
(1)求(﹣7)*(﹣2)的值;
(2)若x1,x2是一元次方程x2﹣5x﹣6=0的两个根,求x1*x2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
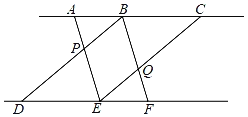
【题目】如图,已知AC∥DF,点B在AC上,点E在DF上,连结AE,BD相交于点P,连结CE,BF相交于点Q,若AB=EF,BC=DE.
(1)求证:四边形BPEQ为平行四边形;
(2)若DP=2BP,BF=3,CE=6.求证:四边形BPEQ为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
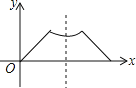
【题目】已知点P为某个封闭图形边界上的一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )
A. 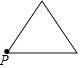 B.
B.  C.
C. 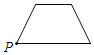 D.
D. 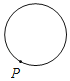
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金秋时节,硕果飘香,某精准扶贫项目果园上市一种有机生态水果.为帮助果园拓宽销路,欣欣超市对这种水果进行代销,进价为5元/千克,售价为6元/千克时,当天的销售量为100千克;在销售过程中发现:销售单价每上涨0.5元,当天的销售量就减少5千克.设当天销售单价统一为x元/千克(x≥6,且x是按0.5元的倍数上涨),当天销售利润为y元.
(1)求y与x的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若该种水果每千克的利润不超过80%,要想当天获得利润最大,每千克售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
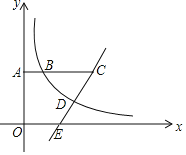
【题目】如图,已知点![]() ,
,![]() ,且点B在双曲线
,且点B在双曲线![]() 上,在AB的延长线上取一点C,过点C的直线交双曲线于点D,交x轴正半轴于点E,且
上,在AB的延长线上取一点C,过点C的直线交双曲线于点D,交x轴正半轴于点E,且![]() ,则线段CE长度的取值范围是
,则线段CE长度的取值范围是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com