
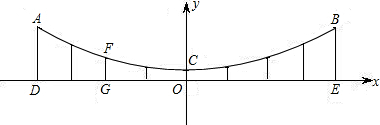
分析 设抛物线的解析式为y=ax2+c,根据题意F(-6,2),C(0,1),由待定系数法就可以得到函数表达式,由相邻两柱之间距离为3m就可以得出OD=12,就有A的横坐标为-12,将A的横坐标为-12代入解析式就可以求出AD的值.
解答 解:由题意得:F(-6,3),C(0,1),
∵点C为抛物线的顶点,
∴设抛物线的关系式为y=ax2+1,
把F(-6,3)代入关系式,得a=$\frac{1}{18}$,
∴y=$\frac{1}{18}$x2+1,
由图可得,点A的横坐标为-12,
∴把x=-12代入关系式得y=9,
即A(-12,9)
∴AD的长度为9米.
点评 本题考查了运用待定系数法求二次函数的解析式的运用,由函数的解析式根据自变量的值求函数值的运用,解答时求出函数的解析式是关键.


科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=28}\\{6(x+y)=200}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=28}\\{10x+6y=200}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=28}\\{6x+y=200}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=28}\\{6x+10y=200}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
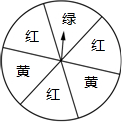 有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:
有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15%-5%=x | B. | 15%-5%=2x | C. | (1-5%)(1+15%)=2(1+x) | D. | (1-5%)(1+15%)=(1+x)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
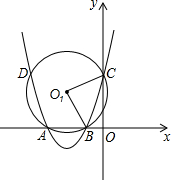 如图,抛物线y=ax2+bx+3过点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1经过A,B,C三点,与抛物线相交于另一点D.
如图,抛物线y=ax2+bx+3过点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1经过A,B,C三点,与抛物线相交于另一点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.43×105 | B. | 0.643×107 | C. | 64.3×105 | D. | 6.43×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com