
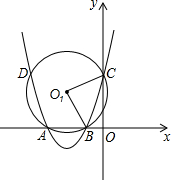
 如图,抛物线y=ax2+bx+3过点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1经过A,B,C三点,与抛物线相交于另一点D.
如图,抛物线y=ax2+bx+3过点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1经过A,B,C三点,与抛物线相交于另一点D.分析 (1)将已知点的坐标代入抛物线的解析式,利用待定系数法确定二次函数的解析式即可;
(2)过O1作O1H⊥x轴得到O1的横坐标为-2,设O1(-2,y),过C作CQ⊥HO1,利用勾股定理得到O1H2+HB2=O1Q2+QC2,从而得到y2+12=(3-y)2+22,
解得:y=2后即可得到O1的坐标;
(3)设F(x,x2+4x+3),分若E、F在AB的同侧和若E、F在AB的异侧,则F与抛物线的顶点重合两种情况即可求得点F的坐标;
(4)当E、F在AB的两侧时,根据四边形AFBE是平行四边形,AB⊥EF,F3(-2,-1)得到EF=2,然后根据AB=2得到四边形AEBF是正方形,求得BF=$\sqrt{2}$.
解答 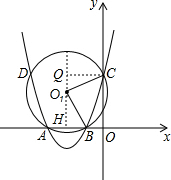 解:(1)∵抛物线y=ax2+bx+3过点A(-3,0),B(-1,0),
解:(1)∵抛物线y=ax2+bx+3过点A(-3,0),B(-1,0),
∴$\left\{\begin{array}{l}{9a-3b+3=0}\\{a-b+3=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=1}\\{b=4}\end{array}\right.$,
∴抛物线的解析式为y=x2+4x+3,对称轴为直线x=-2;
(2)过O1作O1H⊥x轴,
∴AH=HB,
∵OB=1,AB=2,
∴OH=2,
∴O1的横坐标为-2,
设O1(-2,y)过C作CQ⊥HO1,
∵O1B=O1C,
∴O1H2+HB2=O1Q2+QC2,
∴y2+12=(3-y)2+22,
解得:y=2,
∴O1(-2,2);
(3)设F(x,x2+4x+3),
①若E、F在AB的同侧,则EF=AB=2,
∵点E在抛物线的对称轴上,
∴|x+2|=2,
∴x=0或x=-4,
∴F1(0,3),F2(-4,3);
②若E、F在AB的异侧,则F与抛物线的顶点重合,即F3(-2,-1),
∴存在点F1(0,3),F2(-4,3),F3(-2,-1),
∴A、B、E、F为顶点的四边形为平行四边形;
(4)当E、F在AB的两侧时,
∵四边形AFBE是平行四边形,AB⊥EF,F3(-2,-1),
∴EF=2,
又∵AB=2,
∴四边形AEBF是正方形,
∴BF=$\sqrt{2}$.
点评 本题考查了二次函数的综合运用,本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点.主要考查学生数形结合的数学思想方法.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
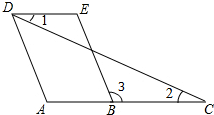 已知,如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
已知,如图,AD∥BE,∠1=∠2,求证:∠A=∠E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 李老师要从包括小明在内的四名班委中,随机抽取2名学生参加学生会选举,抽到小明的概率是$\frac{1}{2}$ | |
| B. | 一组数据6,8,7,8,8,9,10的众数和中位数都是8 | |
| C. | 对甲、乙两名运动员某个阶段的比赛成绩进行分析,甲的成绩数据的方差是S甲2=0.01,乙的成绩数据的方差是S乙2=0.1,则在这个阶段甲的成绩比乙的成绩稳定 | |
| D. | 一个盒子中装有3个红球,2个白球,这些球除颜色外都相同,从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,两次摸到相同颜色的球的概率是$\frac{8}{25}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a6÷a3=a3 | B. | a2•a3=a6 | C. | (a2b)3=a6b | D. | ($\frac{a}{b}$)3=$\frac{{a}^{3}}{b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 种植基地 | 该基地的累积产量占两 基地累积总产量的百分比 | 该基地累积存入仓库的量占 该基地的累积产量的百分比 |
| 甲基地 | 60% | 85% |
| 乙基地 | 40% | 22.5% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com