
| 种植基地 | 该基地的累积产量占两 基地累积总产量的百分比 | 该基地累积存入仓库的量占 该基地的累积产量的百分比 |
| 甲基地 | 60% | 85% |
| 乙基地 | 40% | 22.5% |
分析 (1)根据等量关系“该地累积存入仓库中的量=累积产量分别占两基地累积总产量的百分比×累积存入仓库的量占累积产量的百分比×累积总产量”通过表中的数据用y表示出甲乙两基地累积存入仓库中的量;
(2)根据等量关系“存入仓库的该种农产品总产量=甲基地存入仓库的总产量+乙基地存入仓库的总产量”列出函数关系式;
(3)根据等量关系“该产品库存量=原存入量+收获时存入量-售出量”列出函数关系式并求得最小值.
解答 解:(1)①甲基地累积存入仓库的量:
85%×60%y=0.51y(吨).
②乙基地累积存入仓库的量:
22.5%×40%y=0.09y(吨).
(2)p=0.51y+0.09y=0.6y,
∵y=2x+3,
∴p=0.6(2x+3)=1.2x+1.8.
(3)设在此收获期内仓库库存该种农产品T吨.
T=42.6+p-m
=42.6+1.2x+1.8-(-x2+13.2x-1.6)
=x2-12x+46=(x-6)2+10,
∵1>0,
∴抛物线的开口向上,
又∵1≤x≤10且x为整数,
∴当x=6时,T的最小值为10;
∴在此收获期内连续销售6天,该农产品库存达最低值,最低库存为10吨.
点评 本题主要考查了列函数表达式和运用二次函数的性质求实际问题最值,审清题意正确列出函数表达式是解决问题的关键.


科目:初中数学 来源: 题型:解答题
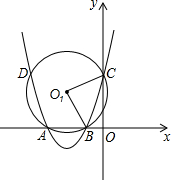 如图,抛物线y=ax2+bx+3过点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1经过A,B,C三点,与抛物线相交于另一点D.
如图,抛物线y=ax2+bx+3过点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1经过A,B,C三点,与抛物线相交于另一点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{6}$<1 | B. | $\root{3}{-8}$=$\root{3}{8}$ | C. | $\sqrt{15}$>4 | D. | $\sqrt{3}$-2>-$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.43×105 | B. | 0.643×107 | C. | 64.3×105 | D. | 6.43×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com