
【题目】(本题满分8分)如图,□ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N。
(1)(4分)求证:四边形CMAN是平行四边形。
(2)(4分)已知DE=4,FN=3,求BN的长。

【答案】(1)详见解析;(2)5.
【解析】
试题分析:(1)通过AE⊥BD,CF⊥BD证明AE∥CF,再由四边形ABCD是平行四边形得到AB∥CD,由两组对边分别平行的四边形是平行四边形可证得四边形CMAN是平行四边形;(2)证明△MDE≌∠NBF,根据全等三角形的性质可得DE=BF=4,再由勾股定理得BN=5.
试题解析:⑴证明:∵AE⊥BD CF⊥BD
∴AE∥CF
又∵四边形ABCD是平行四边形
∴AB∥CD
∴四边形CMAN是平行四边形
⑵由⑴知四边形CMAN是平行四边形
∴CM=AN.
又∵四边形ABCD是平行四边形
∴ AB=CD,∠MDE=∠NBF.
∴AB-AN=CD-CM,即DM=BN.
在△MDE和∠NBF中
∠MDE=∠NBF,∠DEM=∠BFN=90°,DM=BN
∴△MDE≌∠NBF
∴DE=BF=4,
由勾股定理得BN=![]() =
=![]() =5.
=5.
答:BN的长为5.


科目:初中数学 来源: 题型:
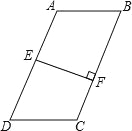
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S= ;
(2)若AB>DC,则此时四边形ABCD的面积S′ S(用“>”或“=”或“<”填空).
查看答案和解析>>
科目:初中数学 来源: 题型:
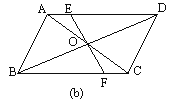
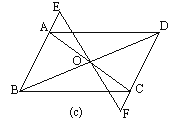
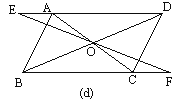
【题目】已知:如图(a),□ABCD的对角线AC、BD相交于点O , EF过点O与AB、CD分别相交于点E、F . 求证:OE=OF , AE=CF , BE=DF . 若上图中的条件都不变,将EF转动到图b的位置,那么上述结论是否成立?若将EF向两方延长与平行四边形的两对边的延长线分别相交(图c和图d),结论是否成立,说明你的理由.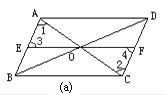
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将1、 ![]() 、
、 ![]() 、
、 ![]() 按如图方式排列,若规定(m,n)表示第m排从左向右第n个数,则(6,5)与(13,6)表示的两数之积是( )
按如图方式排列,若规定(m,n)表示第m排从左向右第n个数,则(6,5)与(13,6)表示的两数之积是( ) 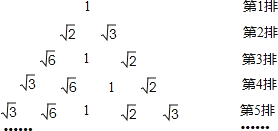
A.![]()
B.6
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com