
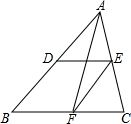
 如图,△ABC中,D、E、F分别是AB、AC、BC的中点.若EF=5cm,则AB=10cm;若BC=9cm,则DE=4.5cm;中线AF与DE的关系互相平分.
如图,△ABC中,D、E、F分别是AB、AC、BC的中点.若EF=5cm,则AB=10cm;若BC=9cm,则DE=4.5cm;中线AF与DE的关系互相平分. 分析 利用三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.可以求得AB、ED的长度;连接DF,易判定四边形ADFE为平行四边形,则该平行四边形的对角线相互平分.
解答 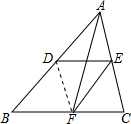 解:∵在△ABC中,点E、F分别是AC、BC的中点,
解:∵在△ABC中,点E、F分别是AC、BC的中点,
∴DE是△ABC的中位线,
∴EF∥AB且EF=$\frac{1}{2}$AB.
又EF=5cm,
∴AB=10cm.
同理,DE=$\frac{1}{2}$BC=4.5cm.
如图,连接DF,
∵AD=EF,AD∥EF,
∴四边形ADFE为平行四边形,
∴中线AF与DE的关系是 互相平分.
故答案是:10、4.5、互相平分.
点评 本题考查了平行四边形的判定与性质,三角形中位线定理.凡是可以用平行四边形知识证明的问题,不要再回到用三角形全等证明,应直接运用平行四边形的性质和判定去解决问题.


科目:初中数学 来源: 题型:解答题
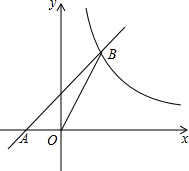 如图,直线y=kx+2k (k≠0)与x轴交于点A,与反比例函数y=(m+3)x2m-1在第一象限内的图象交于点B,已知S△AOB=3.
如图,直线y=kx+2k (k≠0)与x轴交于点A,与反比例函数y=(m+3)x2m-1在第一象限内的图象交于点B,已知S△AOB=3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
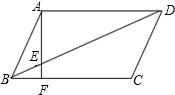 如图,在?ABCD中,∠ABC=72°,AF⊥BC于F,AF交BD于点E,若DE=2AB,则∠AED的大小是( )
如图,在?ABCD中,∠ABC=72°,AF⊥BC于F,AF交BD于点E,若DE=2AB,则∠AED的大小是( )| A. | 60° | B. | 66° | C. | 70° | D. | 72° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
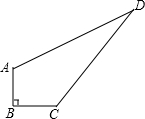 老张家有一块草坪如图所示.家里想整理它,需要知道其面积.老张测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请你帮老张家计算一下这块草坪的面积.
老张家有一块草坪如图所示.家里想整理它,需要知道其面积.老张测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请你帮老张家计算一下这块草坪的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com