
【题目】如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一动点(不与点A,B重合),DP交AC于点Q.
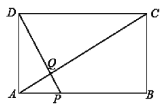
(1)求证:△APQ∽△CDQ;
(2)当PD⊥AC时,求线段PA的长度;
(3)当点P在线段AC的垂直平分线上时,
求sin∠ CPB的值.
【答案】(1)证明见解析;(2)PA=![]() ;(3)sin∠ CPB=
;(3)sin∠ CPB=![]() .
.
【解析】
试题分析:(1)利用两角对应相等的两个三角形易判断△APQ∽△CDQ;(2)由条件可推出△APD∽△DAC,得出![]() ,代入数值可求出PA的值;(3)由勾股定理能够求出PC的长度,再在Rt△CBP中求sin∠ CPB的值.
,代入数值可求出PA的值;(3)由勾股定理能够求出PC的长度,再在Rt△CBP中求sin∠ CPB的值.
试题解析:(1)∵四边形ABCD是矩形,∴AB∥CD,∴∠CAB=∠DCA,∠APQ=∠CDQ,∴△APQ∽△CDQ .
(2)PD⊥AC,∴∠ACD+∠PDC=90° ,∵∠PDA+∠PDA=90°,∴∠ACD=∠PDA,∵∠ADC=∠PAD=90°,∴△ADC∽△PDA,∴![]() ,
,![]() ,∴PA=
,∴PA=![]() .(3)当点P在线段AC的垂直平分线上时,PA=PC.设PA=x,则PB=10-x.又在矩形ABCD中,∠B=90°,∴
.(3)当点P在线段AC的垂直平分线上时,PA=PC.设PA=x,则PB=10-x.又在矩形ABCD中,∠B=90°,∴![]() ,∴
,∴![]() .解得:x=
.解得:x=![]() ,∴PC=PA=
,∴PC=PA=![]() .∴sin∠CPB=
.∴sin∠CPB=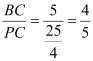


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
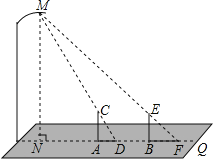
【题目】晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
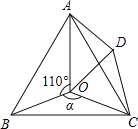
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课前预习是学习数学的重要环节,为了了解所教班级学生完成数学课前预习的具体情况,王老师对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
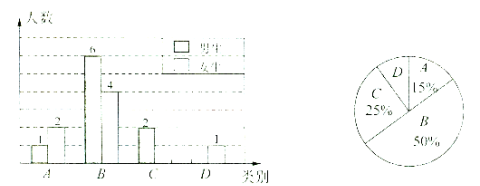
(l) 王老师一共调查了多少名同学?
(2) C类女生有多少名?D类男生有多少名?并将上面条形统计图补充完整;
(3) 为了共同进步,王老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学中男同学不少于1人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(a,b)和点Q(a,b′),给出如下定义:
若![]() ,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5).
,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5).
(1)①点(![]() ,1)的限变点的坐标是 ;
,1)的限变点的坐标是 ;
②在点A(-2,-1),B(-1,2)中有一个点是函数y=![]() 图象上某一个点的限变点,这个点是 ;
图象上某一个点的限变点,这个点是 ;
(2)若点P在函数y=-x+3(-2≤x≤k,k>-2)的图象上,其限变点Q的纵坐标b′的取值范围是-5≤b′≤2,求k的取值范围;
(3)若点P在关于x的二次函数y= x2-2tx+t2+t的图象上,其限变点Q的纵坐标b′的取值范围是b′≥m或b′<n,其中m>n.令s=m-n,求s关于t的函数解析式并直接写出s的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com