
【题目】如图,在直角坐标系中,矩形OABC的顶点C在x轴的负半轴上,点A在y轴正半轴上,矩形OABC的面积为8![]() .把矩形OABC沿DE翻折,使点B与点O重合,点C落在第三象限的G点处,作EH⊥x轴于H,过E点的反比例函数y=
.把矩形OABC沿DE翻折,使点B与点O重合,点C落在第三象限的G点处,作EH⊥x轴于H,过E点的反比例函数y=![]() 图象恰好过DE的中点F.则k=_____,线段EH的长为:_____.
图象恰好过DE的中点F.则k=_____,线段EH的长为:_____.

【答案】-2![]() 2
2![]()
【解析】
连接BO与ED交于点Q,过点Q作QG⊥x轴,垂足为G,可通过三角形全等证得BO与ED的交点就是ED的中点F,由相似三角形的性质可得S△OGF=![]() S△OCB,根据反比例函数比例系数的几何意义可求出k,从而求出S△OAE,进而可以得到AB=4AE,即BE=3AE.由轴对称的性质可得OE=BE,从而得到OE=3AE,也就有AO=2
S△OCB,根据反比例函数比例系数的几何意义可求出k,从而求出S△OAE,进而可以得到AB=4AE,即BE=3AE.由轴对称的性质可得OE=BE,从而得到OE=3AE,也就有AO=2![]() AE,根据△OAE的面积可以求出AE,OA的值.易证四边形OAEH为矩形,从而得到EH=OA,就可求出EH的值.
AE,根据△OAE的面积可以求出AE,OA的值.易证四边形OAEH为矩形,从而得到EH=OA,就可求出EH的值.
解:连接BO与ED交于点Q,过点Q作QN⊥x轴,垂足为N,如图所示,

∵矩形OABC沿DE翻折,点B与点O重合,
∴BQ=OQ,BE=EO.
∵四边形OABC是矩形,
∴AB∥CO,∠BCO=∠OAB=90°.
∴∠EBQ=∠DOQ.
在△BEQ和△ODQ中,
 .
.
∴△BEQ≌△ODQ(ASA).
∴EQ=DQ.
∴点Q是ED的中点.
∵∠QNO=∠BCO=90°,
∴QN∥BC.
∴△ONQ∽△OCB.
∴![]() .
.
∴S△ONQ=![]() S△OCB.
S△OCB.
∵S矩形OABC=8![]() ,
,
∴S△OCB=S△OAB=4![]() .
.
∴S△ONQ=![]() .
.
∵点F是ED的中点,
∴点F与点Q重合.
∴S△ONF=![]() .
.
∵点F在反比例函数y=![]() 上,
上,
∴![]() =
=![]() .
.
∵k<0,
∴k=﹣2![]() .
.
∴S△OAE=![]() =
=![]() .
.
∵S△OAB=4![]() ,
,
∴AB=4AE.
∴BE=3AE.
由轴对称的性质可得:OE=BE.
∴OE=3AE.OA=![]() =2
=2![]() AE.
AE.
∴S△OAE=![]() AOAE=
AOAE=![]() ×2
×2![]() AE×AE=
AE×AE=![]() .
.
∴AE=1.
∴OA=2![]() ×1=2
×1=2![]() .
.
∵∠EHO=∠HOA=∠OAE=90°,
∴四边形OAEH是矩形.
∴EH=OA=2![]() .
.
故答案分别为:﹣2![]() 、2
、2![]() .
.


科目:初中数学 来源: 题型:
【题目】某路段上有A,B两处相距近200m且未设红绿灯的斑马线.为使交通高峰期该路段车辆与行人的通行更有序,交通部门打算在汽车平均停留时间较长的一处斑马线上放置移动红绿灯.图1,图2分别是交通高峰期来往车辆在A,B斑马线前停留时间的抽样统计图.根据统计图解决下列问题:
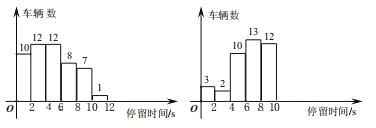
(1)若某日交通高峰期共有350辆车经过A斑马线,请估计该日停留时间为10s~12s的车辆数,以及这些停留时间为10s~12s的车辆的平均停留时间;(直接写出答案)
(2)移动红绿灯放置在哪一处斑马线上较为合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
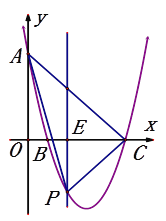
【题目】在平面直角坐标系中,抛物线![]() 与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).
与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).
(1)当b=1时,求抛物线相应的函数表达式;
(2)当b=1时,如图,E(t,0)是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P.求△APC面积的最大值;
(3)当c =b+ n.时,且n为正整数.线段BC(包括端点)上有且只有五个点的横坐标是整数,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是
是![]() 的角平分线,点
的角平分线,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,
,![]()
(1)如图1,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,若![]() 为等边三角形,在不添加辅助线的情况下,请你直接写出所有的全等三角形.
为等边三角形,在不添加辅助线的情况下,请你直接写出所有的全等三角形.
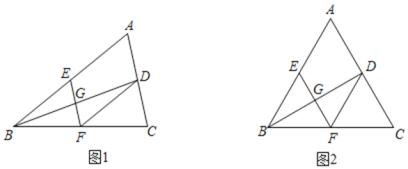
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低。马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种 | A | B |
原来的运费 | 45 | 25 |
现在的运费 | 30 | 20 |
(1)求每次运输的农产品中A,B产品各有多少件?
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() .与
.与![]() 轴交于点C,且O,C两点之间的距离为3,
轴交于点C,且O,C两点之间的距离为3,![]() ,
,![]() ,点A,C在直线
,点A,C在直线![]() 上.
上.
(1)求点C的坐标;
(2)当![]() 随着
随着![]() 的增大而增大时,求自变量
的增大而增大时,求自变量![]() 的取值范围;
的取值范围;
(3)将抛物线![]() 向左平移
向左平移![]() 个单位,记平移后
个单位,记平移后![]() 随着
随着![]() 的增大而增大的部分为P,直线
的增大而增大的部分为P,直线![]() 向下平移n个单位,当平移后的直线与P有公共点时,求
向下平移n个单位,当平移后的直线与P有公共点时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种工业原料,甲仓库有12吨,乙仓库有6吨,现需从甲、乙两仓库将这种工业原料分别调往A工厂10吨,B工厂8吨,已知从甲仓库调运1吨原料到A,B两工厂的运费分别是40元和80元,从乙仓库调运1吨原料到A,B两工厂的运费分别是30元和50元.
(1)若总运费为900元,则从甲仓库调运到A工厂的原料为多少吨?
(2)要使总运费最低,应如何安排调运方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
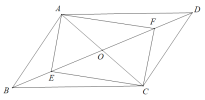
【题目】如图,平行四边形ABCD中,AC、BD相交于点O,E、F是对角线BD上的点,且BE=DF,连接AE、CE、CF、AF.
(1)求证:AE=CF;
(2)若平行四边形ABCD的面积是12,△OCF的面积是2,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0. 其中正确的是( )
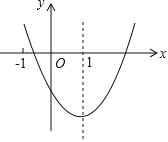
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com