
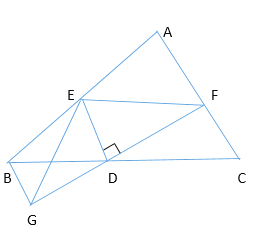
【题目】如图,在△ABC中,D是BC中点,过点D的直线GF交AC于F,交AC的平行线BG于G,DE⊥DF,交AB于E,连接BG,请你判断BE+CF与EF的大小关系,请说明理由.
科目:初中数学 来源: 题型:
【题目】请阅读下述材料:
下述形式的繁分数叫做有限连分数,其中n是自然数,a0是整数,a1,a2,a3,…,an是正整数:

其中![]() 称为部分商。
称为部分商。
按照以下方式可将任何一个分数转化为连分数的形式:![]() ,则
,则![]() ;考虑
;考虑![]() 的倒数,有
的倒数,有![]() ,从而
,从而 ;再考虑
;再考虑![]() 的倒数,有
的倒数,有![]() ,于是得到a的连分数展开式,它有4个部分商:3,1,3,3;
,于是得到a的连分数展开式,它有4个部分商:3,1,3,3;

可利用连分数来求二元一次不定方程的特殊解,以![]() 为例,首先将
为例,首先将![]() 写成连分数的形式,如上所示;其次,数部分商的个数,本例是偶数个部分商(奇数情况请见下例);最后计算倒数第二个渐近分数
写成连分数的形式,如上所示;其次,数部分商的个数,本例是偶数个部分商(奇数情况请见下例);最后计算倒数第二个渐近分数 ,从而
,从而![]() 是一个特解。
是一个特解。
考虑不定方程![]() ,先将
,先将![]() 写成连分数的形式:
写成连分数的形式: 。
。
注意到此连分数有奇数个部分商,将之改写为偶数个部分商的形式:

计算倒数第二个渐近分数: ,所以
,所以![]() 是
是![]() 的一个特解。
的一个特解。
对于分式,有类似的连分式的概念,利用将分数展开为连分数的方法,可以将分式展开为连分式。例如![]() 的连分式展开式如下,它有3个部分商:
的连分式展开式如下,它有3个部分商:![]()
![]() ;
;

再例如, ,它有4个部分商:1,
,它有4个部分商:1,![]() 。
。
请阅读上述材料,利用所讲述的方法,解决下述两个问题
(1)找出两个关于x的多项式p和q,使得![]() 。
。
(2)找出两个关于x的多项式u和v,使得![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某街区的平面示意图,根据要求答题.

(1)这幅图的比例尺是( )
(2)学校位于广场的( )面(填东、南、西、北)( )千米处.
(3)人民公园位于广场的东偏南![]() 方向3千米处.在图中标出它的位置.
方向3千米处.在图中标出它的位置.
(4)广场的西面1千米处,有一条商业街与人民路垂直,在图中画线表示商业街.
查看答案和解析>>
科目:初中数学 来源: 题型:
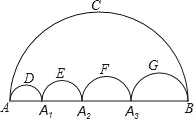
【题目】图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )
A. 甲先到B点 B. 乙先到B点 C. 甲、乙同时到B D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,在平面直角坐标系中S△ABC=24,OA=OB,BC=12.

(1)求出三个顶点坐标.
(2)若P点为y轴上的一动点,且△ABP的面积等于△ABC的面积,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、l1于点D. E(点A. E位于点B的两侧),满足BP=BE,连接AP、CE.
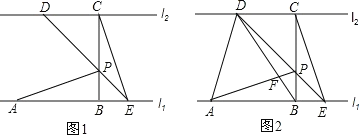
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F. 如图2.
①当![]() =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;
②当![]() =n(n>1)时,设△DAP的面积为S1,△EPC的面积为S2,求
=n(n>1)时,设△DAP的面积为S1,△EPC的面积为S2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2k+3)x+k2+3k+2=0.
(1)判断方程根的情况;
(2)若方程的两根x1,x2满足(x1-1)(x2-1)=5,求k值;
(3)若△ABC的两边AB,AC的长是方程的两根,第三边BC的长为5,
①则k为何值时,△ABC是以BC为斜边的直角三角形?
②k为何值时,△ABC是等腰三角形,并求出△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点D、E分别是△ABC两边AB、BC所在直线上的点,∠BDE+∠ACB=180°,DE=AC,AD=2BD.


(1) 如图1,当点D、E分别在AB、CB的延长线上时,求证:BE=BD
(2) 如图2,当点D、E分别在AB、BC边上时,BE与BD存在怎样的数量关系?请写出你的结论,并证明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景介绍)勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
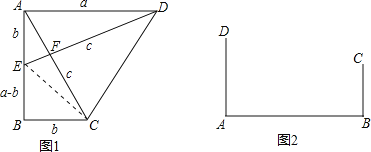
(小试牛刀)把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
(知识运用)(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
(知识迁移)借助上面的思考过程与几何模型,求代数式![]() 最小值(0<x<16)
最小值(0<x<16)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com