练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．$\sqrt{\frac{9}{25}}$=$\frac{3}{5}$．

    分析 直接利用二次根式的性质化简求出答案．

    解答 解：原式=$\sqrt{（\frac{3}{5}）^{2}}$=$\frac{3}{5}$．
    故答案为：$\frac{3}{5}$．

    点评 此题主要考查了二次根式的化简，正确开平方是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．某水果经销商看准商机，第一次用8000元购进某种水果进行销售，销售良好，于是第二次用了24000元购进同种水果，但此次进价比第一次提高了20%，所购数量比第一次购进数量的2倍还多200千克．
    （1）求第一次所购该水果的进货价是每千克多少元？
    （2）在实际销售中，两次售价均相同，但第一次购进的水果在销售过程中，消费者挑选后，由于水果品相下降，最后50千克八折售出；第二次购进的水果由于同样的原因，最后100千克九折售出，若售完这两批水果的获利不低于9400元，则每千克售价至少为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

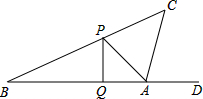    11．如图：小明同学正在操场上放风筝，风筝从A处起飞，几分钟后便飞达C处，此时，在AQ延长线上B处的小亮同学，发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上．
    （1）已知AB为30米，若在B处测得旗杆顶点P的仰角为30°，A处测得点P的仰角为45°，试求旗杆高；
    （2）此时，在A处背向旗杆又测得风筝的仰角为75°，绳子在空中视为一条线段，求绳子AC为多少米？（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

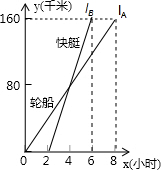    8．如图，一艘轮船（A）和一艘快艇（B）沿相同路线从甲港出发到乙港，图中lA和lB分别表示A、B行驶过程中路程y（km）与时间x（h）变化之间的函数关系，根据图象解答下列问题：
    （1）轮船A的速度是20km/h；快艇B的速度是40km/h；
    （2）求时间x在什么范围时，快艇在轮船的前面；
    （3）求时间x在什么范围时，轮船A、快艇B之间保持的距离不超过10km．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，△ABC，AD平分∠BAC交BC于点D，求证：$\frac{BD}{CD}$=$\frac{AB}{AC}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知点A（m+2，3m-5），求符合下列条件的点A的坐标．
    （1）点A在x轴上；
    （2）点A在y轴上；
    （3）点A在第一象限且到x轴的距离是它到y轴距离的一半．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

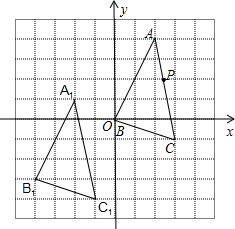    12．在如图的单位正方形网格中，三角形ABC经过平移后得到三角形A1B1C1，已知在AC上一点P（$\frac{12}{5}$，2）平移后的对应点P1，则点P1的坐标为（　　）
    A．（-$\frac{7}{5}$，-1）B．（-$\frac{3}{2}$，-2）C．（-$\frac{8}{5}$，-1）D．（-$\frac{12}{5}$，-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，已知直线a∥b，c⊥d，∠1=36°，则∠2的度数是126°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．先化简，再求值：
    ①（x+1-$\frac{15}{x-1}$）÷$\frac{{x}^{2}-8x+16}{1-x}$，其中x=2；
    ②$（1+\frac{2}{p-2}）$÷$\frac{{p}^{2}-p}{{p}^{2}-4}$，（其中p是满足-3＜p＜3的整数）．

    查看答案和解析>>

    同步练习册答案