
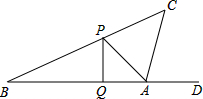
 如图:小明同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.
如图:小明同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.分析 (1)设旗杆高度PQ=x,在RT△APQ中可得AQ=PQ=x,在RT△BPQ中可得BQ=$\sqrt{3}$x,根据AQ+BQ=AB列出方程,解方程可得;
(2)过A作AE⊥BC于E,在Rt△ABE中可得AE=15m,在Rt△CAE中根据sin∠C=$\frac{AE}{AC}$可求得AC.
解答 解:(1)设旗杆的高PQ=xm,
在RT△APQ中,∵∠PAQ=45°,
∴AQ=PQ=x,
在RT△BPQ中,∵∠B=30°,
∴BQ=$\frac{PQ}{tan∠B}$=$\sqrt{3}$x,
∵AQ+BQ=AB,且AB=30,
∴x+$\sqrt{3}$x=30,解得:x=15$\sqrt{3}$-15,
故旗杆高度为(15$\sqrt{3}$-15)m;
(2)过A作AE⊥BC于E,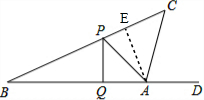
在Rt△ABE中,∵∠B=30°,AB=30m,
∴AE=sin30°×AB=15m,
∵∠CAD=75°,∠B=30°,
∴∠C=45°,
在Rt△CAE中,∵sin∠C=$\frac{AE}{AC}$,
∴AC=$\frac{AE}{sin∠C}$=15$\sqrt{2}$m,
故绳子AC为15$\sqrt{2}$米.
点评 本题考查了仰角、俯角的问题及解直角三角形的应用,解答本题的关键是结合图形构造直角三角形,利用三角函数解直角三角形.


科目:初中数学 来源: 题型:解答题
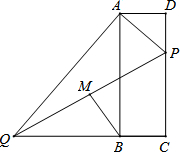 如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2+2 | B. | a2-2 | C. | a4+4 | D. | a4-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.5,6,6.5 | B. | 5,7,10 | C. | $\sqrt{2},\sqrt{3},\sqrt{5}$ | D. | 6,8,10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com