
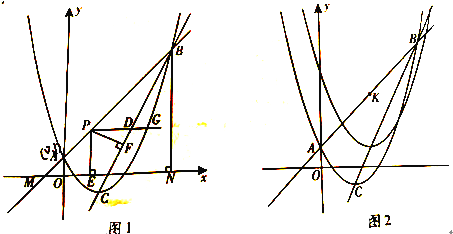
【题目】(2016重庆市第26题)如图1,二次函数![]() 的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD//x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F,当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+![]() BH的值最小,求点H的坐标和GH+
BH的值最小,求点H的坐标和GH+![]() BH的最小值;
BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数![]() 沿直线BC平移,平移的距离是t(t≥0),平移后抛物线使点A,点C的对应点分别为点A’,点C’;当△A’C’K是直角三角形时,求t的值。
沿直线BC平移,平移的距离是t(t≥0),平移后抛物线使点A,点C的对应点分别为点A’,点C’;当△A’C’K是直角三角形时,求t的值。
【答案】(1)、![]() =x+1;
=x+1;![]() =2x-5;(2)、H(5,6);7.5;(3)、t=0或t=4
=2x-5;(2)、H(5,6);7.5;(3)、t=0或t=4![]() 或t=
或t=![]()
【解析】
试题分析:(1)、首先得出点C的坐标,根据△AMO和四边形AONB的面积之比得出△AMO和△BMN的面积之比,从而得出BN=7,然后求出点B的坐标,得出直线AB和直线BC的解析式;(2)、设点P(x0,x0+1),则D(![]() ,x0+1),PE=x0+1,PD=3-0.5x0,根据△PDF∽△BGN得出PE·PF最大时,PE·PD也最大,然后得出PE·PD的函数解析式,根据函数的性质得出点G的坐标,根据△MNB是等腰直角三角形,过B作x轴的平行线,则
,x0+1),PE=x0+1,PD=3-0.5x0,根据△PDF∽△BGN得出PE·PF最大时,PE·PD也最大,然后得出PE·PD的函数解析式,根据函数的性质得出点G的坐标,根据△MNB是等腰直角三角形,过B作x轴的平行线,则![]() BH=B1H,从而得出答案;(3)、令直线BC与x轴交于点I,则I(2.5,0)于是IN=3.5,IN:BN=1:2,则沿直线BC平移时,横坐标平移m时,纵坐标则平移2m,平移后A’(m,1+2m),C’(2+m,-1+2m),然后根据当∠A’KC’=90°,当∠KC’A’=90°和当∠KA’C’=90°三种情况,分别利用勾股定理得出答案.
BH=B1H,从而得出答案;(3)、令直线BC与x轴交于点I,则I(2.5,0)于是IN=3.5,IN:BN=1:2,则沿直线BC平移时,横坐标平移m时,纵坐标则平移2m,平移后A’(m,1+2m),C’(2+m,-1+2m),然后根据当∠A’KC’=90°,当∠KC’A’=90°和当∠KA’C’=90°三种情况,分别利用勾股定理得出答案.
试题解析:(1)、C(2,-1). 由S△AMO:S四边形AONB=1:48,可得由S△AMO:S△BMN=1:49,
所有BN=7,带入二次函数解析式可得B(6,7)。 所以![]() =x+1;
=x+1;![]() =2x-5.
=2x-5.
(2)、设点P(x0,x0+1),则D(![]() ,x0+1),则PE=x0+1,PD=3-0.5x0,
,x0+1),则PE=x0+1,PD=3-0.5x0,
由于△PDF∽△BGN,所以PF:PD的值固定,于是PE·PF最大时,PE·PD也最大,
PE·PD=(x0+1)(3-0.5x0)=![]() ,所以当x0=2.5时,PE·PD最大,即PE·PF最大。
,所以当x0=2.5时,PE·PD最大,即PE·PF最大。
此时G(5,3.5)
可得△MNB是等腰直角三角形,过B作x轴的平行线,则![]() BH=B1H,
BH=B1H,
GH+![]() BH的最小值转化为求GH+HB1的最小值,
BH的最小值转化为求GH+HB1的最小值,
所以当GH和HB1在一条直线上时,GH+HB1的值最小,此时H(5,6),最小值为7-3.5=3.5
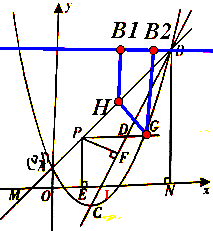
(3)、令直线BC与x轴交于点I,则I(2.5,0)于是IN=3.5,IN:BN=1:2,
所以沿直线BC平移时,横坐标平移m时,纵坐标则平移2m,平移后A’(m,1+2m),C’(2+m,-1+2m),
则A’C’2=8,A’K2=5m2-18m+18,C’K2=5m2-22m+26,
①、当∠A’KC’=90°时,A’K2+KC’2=A’C’2,解得m=![]() ,此时t=
,此时t=![]() ;
;
②、当∠KC’A’=90°时,KC’2+A’C’2=A’K2,解得m=4,此时t=![]() ;
;
③、当∠KA’C’=90°时,A’C’2+A’K2=KC’2,解得m=0,此时t=0
综上所述:t=0或t=4![]() 或t=
或t=![]()


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,都是由边长为1的正方体叠成的立体图形,例如第(1)个图形由1个正方体叠成,第(2)个图形由4个正方体叠成,第(3)个图形由10个正方体叠成,依次规律,第(6)个图形由( )个正方体叠成.
![]()
![]()

 ……
……
A. 36 B. 37 C. 56 D. 84
查看答案和解析>>
科目:初中数学 来源: 题型:
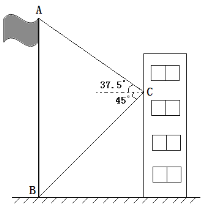
【题目】如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°.升旗时,国旗上端悬挂在距地面2.25米处. 若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?
(参考数据:sian37°=0.60,cos37°=0.80,tan37°=0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com