
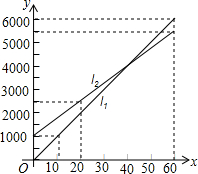
 如图,l1反映了某个体服装老板销售收入y(元)与销售量x(件)之间的关系,l2反映了该老板怒饭的销售成本与销售成本之间的关系,根据图象填空:
如图,l1反映了某个体服装老板销售收入y(元)与销售量x(件)之间的关系,l2反映了该老板怒饭的销售成本与销售成本之间的关系,根据图象填空:分析 (1)当x=60时,所对应的l1上的纵坐标的值为6000,l2上的纵坐标的值为5500;
(2)利用待定系数法分别求出l1,l2的函数解析式,把x=30代入解析式,求出y的值,即可解答;
(3)由(2)即可解答;
(4)销售收入等于销售成本应该看两个函数图象的交点所对应的x的值;
(4)该店赢利应该是销售收入大于销售成本,即l1高于l2;该店亏本.应该是销售收入小于销售成本,即l1低于l2.
解答 解:(1)当销售量为60件时,销售收入为6000元,销售成本为5500元,故答案为:6000,5500;
(2)设l1函数解析式为y1=k1x,
把(60,6000)代入y1=k1x,得:
60k1=6000,
解得:k1=100,
∴y1=100x,
当x=30时,y1=3000,
设l2的函数解析式为:y2=k2x+b,
把(0,1000)(20,2500)代入y2=k2x+b,得:
$\left\{\begin{array}{l}{0+b=1000}\\{20{k}_{2}+b=2500}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{k}_{2}=75}\\{b=1000}\end{array}\right.$
∴y2=75x+1000,
当x=30时,y2=75×30+100=3250,
故答案为:3000,3250.
(3)由(2)可得:l1对应的函数表达式是:y=100x.l2对应的函数表达式是:y=75x+1000.
故答案为:y=100x,y=75x+1000.
(4)由题意可得:75x+1000=100x,
解得:x=40,
当销售量为40件时,销售收入等于销售成本;
故答案为:40.
(5)由函数图象,可得:
当销售量大于40件时,该老板赢利,当销售量小于40件时,该老板亏本.
故答案为:大于40,小于40.
点评 本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,先观察图形,然后填空:
如图,先观察图形,然后填空:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
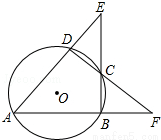 如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )
如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )| A. | α+β | B. | $\frac{α+β}{2}$ | C. | 180°-α-β | D. | $\frac{180°-α-β}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
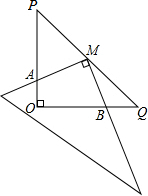 如图,在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
如图,在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com