
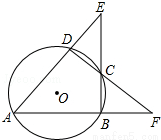
 如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )
如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )| A. | α+β | B. | $\frac{α+β}{2}$ | C. | 180°-α-β | D. | $\frac{180°-α-β}{2}$ |
分析 连结EF,如图,根据圆内接四边形的性质得∠ECD=∠A,再根据三角形外角性质得∠ECD=∠1+∠2,则∠A=∠1+∠2,然后根据三角形内角和定理有∠A+∠1+∠2+∠E+∠F=180°,即2∠A+α+β=180°,再解方程即可.
解答 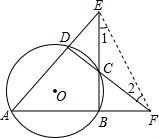 解:连结EF,如图,
解:连结EF,如图,
∵四边形ABCD为圆的内接四边形,
∴∠ECD=∠A,
∵∠ECD=∠1+∠2,
∴∠A=∠1+∠2,
∵∠A+∠1+∠2+∠E+∠F=180°,
∴2∠A+α+β=180°,
∴∠A=$\frac{180°-α-β}{2}$.
故选D.
点评 本题考查了圆内接四边形的性质:圆内接四边形的对角互补;圆内接四边形的性质是沟通角相等关系的重要依据,在应用此性质时,要注意与圆周角定理结合起来.在应用时要注意是对角,而不是邻角互补.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
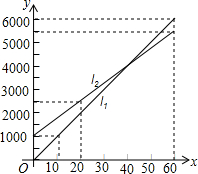 如图,l1反映了某个体服装老板销售收入y(元)与销售量x(件)之间的关系,l2反映了该老板怒饭的销售成本与销售成本之间的关系,根据图象填空:
如图,l1反映了某个体服装老板销售收入y(元)与销售量x(件)之间的关系,l2反映了该老板怒饭的销售成本与销售成本之间的关系,根据图象填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
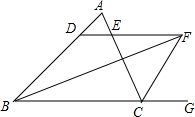 如图,在△ABC中,已知∠ABC和△ABC的外角∠ACG的平分线交于点F,过点F作FD∥BC,FD分别交AB、AC于点D、E,求证:DE=BD-CE.
如图,在△ABC中,已知∠ABC和△ABC的外角∠ACG的平分线交于点F,过点F作FD∥BC,FD分别交AB、AC于点D、E,求证:DE=BD-CE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
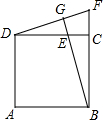 如图所示,在正方形ABCD中,E为CD上一点,延长BC至F,使CF=CE,连接DF,BE与DF相交于点G,则下面结论错误的是( )
如图所示,在正方形ABCD中,E为CD上一点,延长BC至F,使CF=CE,连接DF,BE与DF相交于点G,则下面结论错误的是( )| A. | BE=DF | B. | BG⊥DF | C. | ∠F+∠CEB=90° | D. | ∠FDC+∠ABG=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-16}$=-4 | B. | $\sqrt{16}$=±4 | C. | $\sqrt{(-4)^{2}}$=-4 | D. | $\root{3}{(-4)^{3}}$=-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com