
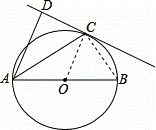
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
(1)求证:AD⊥DC;
(2)若AD=2,AC= ,求AB的长.
,求AB的长.

考点: 切线的性质;相似三角形的判定与性质.
专题: 综合题;压轴题.
分析: (1)连接OC,根据切线的性质得到OC与CD垂直,进而得到∠OCA+∠DCA=90°,由AC为角平分线,根据角平分线定义得到两个角相等,又OA=OC,根据等边对等角得到又得到另两个角相等,等量代换后得到∠DAC=∠OCA,根据等角的余角相等得到∠DCA+∠DAC=90°,从而得到∠ADC为直角,得证;
(2)连接CB,由AB为圆O的直径,根据直径所对的圆周角为直角得到∠ACB与∠ADC相等都为直角,又根据AC为角平分线得到一对角相等,由两对对应角相等的两三角形相似,得到三角形ADC与三角形ABC相似,由相似得比例列出关系式,把AC和AD的长即可求出AB的长.
解答: 解:(1)连接OC,
∵直线CD与⊙O相切于点C,
∴OC⊥CD.
∴∠OCA+∠DCA=90°,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
又∵在⊙O中,OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴∠DCA+∠DAC=90°,
则∠ADC=90°,
即AD⊥DC;
(2)连接BC.
∵AB为圆O的直径,
∴∠ACB=90°,
∴∠ADC=∠ACB=90°,
又∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴△ADC∽△ACB,
∴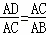 ,即
,即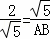 ,
,
则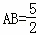 .
.
点评: 此题考查了切线的性质,圆周角定理以及相似三角形的判定与性质.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.同时要求学生掌握直径所对的圆周角为直角.圆与相似三角形及三角函数相融合的解答题、与切线的性质和判定有关的证明题是近几年中考的热点试题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
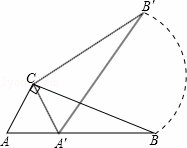
如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )
A. 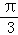 B.
B. 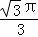 C.
C. 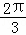 D. π
D. π
查看答案和解析>>
科目:初中数学 来源: 题型:
从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 100 400 800 1000 2000 5000
发芽种子粒数 85 298 652 793 1604 4005
发芽频率 0.850 0.745 0.815 0.793 0.802 0.801
根据以上数据可以估计,该玉米种子发芽的概率约为 (精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场出售一批进价为2元的贺卡,在市场营销中发现,此商品的日销售单价x(单位:元)与日销售数量y(单位:张)之间有如下关系:
销售单价x(元) 3 4 5 6
日销售量y(张) 20 15 12 10
(1)根据表中数据在平面直角坐标系中描出实数对(x,y)的对应点;
(2)确定y与x之间的函数关系式,并画出图象;
(3)设销售此贺卡的日纯利润为w元,试求出w与x之间的函数关系式.若物价局规定该贺卡售价最高不超过10元/张,请你求出日销售单价x定为多少元时,才能获得最大日销售利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com