
����Ŀ����1����ͼ1��![]() �ǵȱ�������
�ǵȱ�������![]() ��
��![]() ��һ���㣨��
��һ���㣨��![]() �����
�����![]() ���غϣ�����
���غϣ�����![]() ����
����![]() ����
Ϊ����![]() �Ϸ����ȱ�������
�Ϸ����ȱ�������![]() ������
������![]() �����ܷ���
�����ܷ���![]() ��
��![]() ֮���������ϵ�𣿲�֤���㷢�ֵĽ��ۣ�
֮���������ϵ�𣿲�֤���㷢�ֵĽ��ۣ�
��2����ͼ����������![]() �ڵȱ�������
�ڵȱ�������![]() ��
��![]() ���˶�ʱ����
���˶�ʱ����![]() ���
���![]() ���غϣ�������
���غϣ�������![]() ����
����![]() Ϊ�������Ϸ����·��ֱ����ȱ�������
Ϊ�������Ϸ����·��ֱ����ȱ�������![]() �͵ȱ�������
�͵ȱ�������![]() ������
������![]() ��
��![]() ��̽��
��̽��![]() ��
��![]() ��
��![]() �к�������ϵ����֤����̽���Ľ��ۣ�
�к�������ϵ����֤����̽���Ľ��ۣ�
��3����ͼ����������![]() �ڵȱ�������
�ڵȱ�������![]() ��
��![]() ���ӳ������˶�ʱ������������ͼ2��ͬ����
���ӳ������˶�ʱ������������ͼ2��ͬ����![]() ����ֱ��д��
����ֱ��д��![]() ����������
����������

���𰸡���1��![]() ����2��
����2��![]() ����3��6
����3��6
��������
��1���ɵȱ������ε����ʿɵ�AC=BC��DC=CE����ACB=��DCE=60�����ɵá�ACE=��BCD��������SAS����֤��BCD�ա�ACE����AE=BE��
��2���ɵȱ������ε����ʿɵ�AC=BC��DC=CF����ACB=��DCF=60�����ɵá�FCB=��DCA��������SAS����֤��ACD�ա�BCF����BF=AD�����ɵ�AB=AE=BF��
��3�����ݵȱ������ε����ʺ�ȫ�������ε��ж������ʿɵ�AE=BD��BF=AD��������AB�ij���
�⣺��1��AE=BD,�������£�
�ߡ�ABC����DCE�ǵȱ�������
��AC=BC��DC=CE����ACB=��DCE=60����
���ACE=��BCD����AC=BC��DC=CE
���BCD�ա�ACE��SAS��
��AE=BD
��2��AB=AE+BF��
�������£��ߡ�ABC����DCF�ǵȱ������Σ�
��AC=BC��CF=CD����FCD=��BCA=60����
���FCB=��DCA����AC=BC��CF=CD��
���ACD�ա�BCF��SAS��
��BF=AD��
�ɣ�1����֪��BD=AE��
��AB=BD+AD��
��AB=AE+BF
��3���ߡ�ABC����DCE�ǵȱ������Σ�
��AC=BC��DC=CE����ACB=��DCE=60����
���BCD=��ACE����AC=BC��DC=CE��
���BCD�ա�ACE��SAS��
��AE=BD=8��
�ߡ�ABC����DCF�ǵȱ������Σ�
��AC=BC��CF=CD����FCD=��BCA=60����
���FCB=��DCA����AC=BC��CF=CD��
���ACD�ա�BCF��SAS��
��BF=AD=2��
��AB=BD-AD
��AB=8-2=6.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A�ں���y= ![]() ��x��0����ͼ���ϣ���OA=4������A��AB��x���ڵ�B�����ABO���ܳ�Ϊ ��
��x��0����ͼ���ϣ���OA=4������A��AB��x���ڵ�B�����ABO���ܳ�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,����ABC����ijһ����ƽ��һ���ľ���õ���MNL,�����н�������ȷ�������� ��
��AM��BN����AM=BN����BC=ML���ܡ�ACB=��MNL��

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+2��ͼ����x�ύ�ڵ�A����1��0����B��4��0������y�ύ�ڵ�C��
��1��a=��b=��
��2����PΪ�ú����ڵ�һ�����ڵ�ͼ���ϵ�һ�㣬����P��PQ��BC�ڵ�Q������PC��
�����߶�PQ�����ֵ��
������P��C��QΪ��������������ABC���ƣ����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������˾������ 960 ���²�Ʒ��Ҫ���ӹ�����Ͷ���г����ּס���������������ӹ�������Ʒ����֪���������ӹ����������Ʒ���ҹ��������ӹ����������Ʒ���� 20 �죬������ÿ��ӹ����������ҹ���ÿ��ӹ���������![]() ����˾�踶�����ӹ�����Ϊÿ�� 80 Ԫ���ҹ����ӹ�����Ϊÿ�� 120 Ԫ��
����˾�踶�����ӹ�����Ϊÿ�� 80 Ԫ���ҹ����ӹ�����Ϊÿ�� 120 Ԫ��
��1���ס�����������ÿ����ܼӹ����ټ��²�Ʒ��
��2����˾�ƶ���Ʒ�ӹ��������£�������ÿ�����ҵ�����ɣ�Ҳ�������������Һ�����ɣ��ڼӹ������У���˾��һ������ʦÿ�쵽�����м���ָ����������ÿ�� 15 Ԫ����Ͳ����ѣ� ����﹫˾ѡ��һ�ּ�ʡʱ��ʡǮ�ļӹ���������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=9��BC=12����Rt��DEF�У���DFE=90�㣬EF=6��DF=8��E��F������BC���ϣ�DE��DF���߷ֱ���AB�߽��ڵ�G��H���̶���ABC��������DEF�ӵ�F���B�غϵ�λ�ó�������BC����ÿ��1����λ���ٶ����C�˶���ͬʱ��P�ӵ�F������������FD��DE����ÿ��2����λ���ٶ����E�˶�������E�����Cʱ����DEF�͵�Pͬʱֹͣ�˶������˶�ʱ��Ϊt���룩��
��1����t=2ʱ��PH=cm��DG=cm��
��2����tΪ��ֵʱ����PDGΪ���������Σ���˵�����ɣ�
��3����tΪ��ֵʱ����P���G�غϣ�д��������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ������С�˶�����ȡ�ýϺóɼ����˶�Ա������400ԪǮ����ס������ֽ�Ʒ��30�������м��ֽ�Ʒÿ��16Ԫ�����ֽ�Ʒÿ��12Ԫ����������ֽ�Ʒ������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У��Ա�AB�ϵ�һ��OΪԲ�ģ���OA�ij�Ϊ�뾶��Բ����AB�ڵ�D��BC���O�����ڵ�C������O�İ뾶Ϊ5����A=20�㣬�� ![]() �ij�Ϊ ��
�ij�Ϊ �� 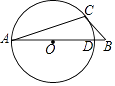
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ABCDE����ijƽ��ֱ������ϵ��������A��B��C��D������ֱ��ǣ�0��a��������3��2������b��m������c��m�������E�������ǣ� ��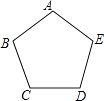
A.��2����3��
B.��2��3��
C.��3��2��
D.��3����2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com