练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平行四边形ABCD中，BE、CE分别平分∠ABC、∠BCD，E在AD上，BE =12，CE =5，则平行四边形ABCD的周长是______．

    【答案】39

    【解析】试题分析：根据角平分线的性质可得：∠BCE=∠DCE，∠ABE=∠EBC，根据平行线的性质可得：∠BCE=∠DEC，∠AEB=∠EBC，则△ECD和△ABE为等腰三角形，则CD=DE，AB=AE，设CD=x，则AB=x，AD=AE+DE=2x，根据平行四边形性质可得：∠ABC+∠BCD=180°，则∠EBC+∠ECB=90°，则△BEC为直角三角形，根据勾股定理可知：BC=13，即2x=13，解得：x=6.5，则四边形ABCD的周长为：6x=6×6.5=39.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AC平分∠BAD，过点C作CE⊥AB于点E，且CD＝CB，∠ABC＋∠ADC＝180°.求证：AE＝(AB＋AD)．

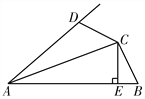
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知四边形ABCD是平行四边形，下列结论中不正确的是(　　)

    A. 当AB＝BC时，它是菱形 B. 当AC⊥BD时，它是菱形

    C. 当∠ABC＝90°时，它是矩形 D. 当AC＝BD时，它是正方形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校计划组织师生参加哈尔滨冰雪节，感受冰雪艺术的魅力．出租公司现有甲、乙两种型号的客车可供租用，且每辆乙型客车的租金比每辆甲型客车少60元．若该校租用3辆甲种客车，4辆乙种客车，则需付租金1720元．

    （1）该出租公司每辆甲、乙两型客车的租金各为多少元？

    （2）若学校计划租用6辆客车，租车的总租金不超过1560元，那么最多租用甲型客车多少辆？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图直线y=x+2与抛物线y=ax2交于A．B两点，点B的坐标（3，m），直线AB交y轴于点C．

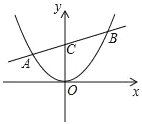
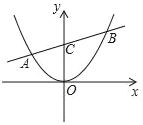
    （1）求a，m的值；

    （2）点P在对称轴右侧的抛物线上，设P点横坐标为t，△PAB的面积为s，求s与t的函数关系式；

    （3）在（2）的条件下，在x轴上有一点Q，当以B．C．P．Q为顶点的四边形是平行四边形时，求点Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）在菱形ABCD中，E，F分别是BC，CD上的点，且CE=CF

    (1)求证：△ABE≌△ADF

    (2)过点C作CG‖EA交AF于点H,交AD于点G，若∠BAE=25°,∠BCD=130°,求∠AHC

    的度数。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形A1B1C1D1；把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2（如图（2））；正方形A2B2C2D2的面积为________，以此下去…，则正方形AnBnCnDn的面积为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(本题满分10分）如图，在四边形ABCD中，AD∥BC，点E在BC的延长线上，CE=BC，连接AE，交CD边于点F，且CF=DF．（1）求证：AD=BC；（2）连接BD、DE，若BD⊥DE，求证：四边形ABCD为菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小颖和小强上山游玩，小颖乘坐缆车，小强步行，两人相约在山顶的缆车终点会和，已知小强行走到缆车终点的路程是缆车到山顶的线路长的倍，小颖在小强出发后分才乘上缆车，缆车的平均速度为米/分，若图中的折线表示小强在整个行走过程中的路程（米）与出发时间（分）之间的关系的图像，请回答下列问题.

    （1）小强行走的总路程是 米，他途中休息了 分；

    （2）分别求出小强在休息前和休息后所走的两段路程的速度；

    （3）当小颖到达缆车终点时，小强离缆车终点的路程是多少？

    查看答案和解析>>

    同步练习册答案