
【题目】如图,点A是抛物线![]() 对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.
对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.
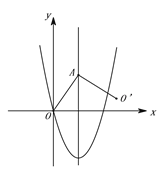
【答案】(2,2)或(2,-1)
【解析】
∵抛物线y=x2-4x对称轴为直线x=-![]()
∴设点A坐标为(2,m),
如图所示,作AP⊥y轴于点P,作O′Q⊥直线x=2,
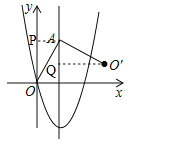
∴∠APO=∠AQO′=90°,
∴∠QAO′+∠AO′Q=90°,
∵∠QAO′+∠OAQ=90°,
∴∠AO′Q=∠OAQ,
又∠OAQ=∠AOP,
∴∠AO′Q=∠AOP,
在△AOP和△AO′Q中,
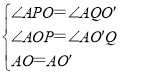
∴△AOP≌△AO′Q(AAS),
∴AP=AQ=2,PO=QO′=m,
则点O′坐标为(2+m,m-2),
代入y=x2-4x得:m-2=(2+m)2-4(2+m),
解得:m=-1或m=2,
∴点A坐标为(2,-1)或(2,2),
故答案是:(2,-1)或(2,2).


科目:初中数学 来源: 题型:
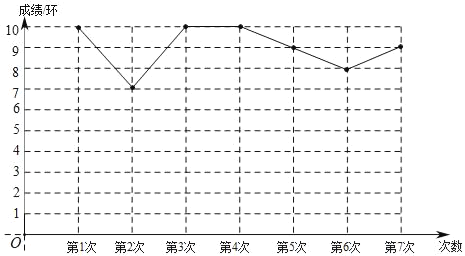
【题目】嘉淇同学利用业余时间进行射击训练,一共射击7次,经过统计,制成如图12所示的折线统计图.
(1)这组成绩的众数是 ;
(2)求这组成绩的方差;
(3)若嘉淇再射击一次(成绩为整数环),得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数,求第8次的射击成绩的最大环数.
查看答案和解析>>
科目:初中数学 来源: 题型:
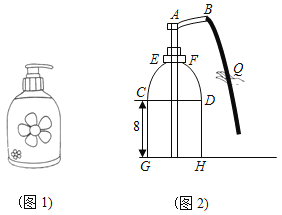
【题目】小林家的洗手盘台面上有一瓶洗手液(如图1).当手按住顶部A下压如图2位置时,洗手液瞬间从喷口B流出路线呈抛物线经过C与E两点.瓶子上部分是由弧![]() 和弧
和弧![]() 组成,其圆心分别为D,C.下部分的是矩形CGHD的视图,GH=10cm,点E到台面GH的距离为14cm,点B距台面的距离为16cm,且B,D,H三点共线.若手心距DH的水平距离为2cm去接洗手液时,则手心距水平台面的高度为_____cm.
组成,其圆心分别为D,C.下部分的是矩形CGHD的视图,GH=10cm,点E到台面GH的距离为14cm,点B距台面的距离为16cm,且B,D,H三点共线.若手心距DH的水平距离为2cm去接洗手液时,则手心距水平台面的高度为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为

A. ![]() B. 5C. 3D.
B. 5C. 3D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中的弦BC等于⊙O的半径,延长BC到D,使BC=CD,点A为优弧BC上的一个动点,连接AD,AB,AC,过点D作DE⊥AB,交直线AB于点E,当点A在优弧BC上从点C运动到点B时,则DE+AC的值的变化情况是( )
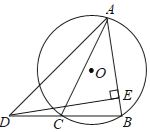
A.不变B.先变大再变小C.先变小再变大D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
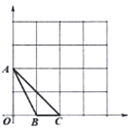
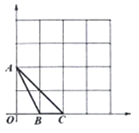
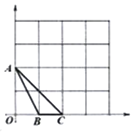
【题目】如图,在下列![]() (边长为1)的网格中,已知
(边长为1)的网格中,已知![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 在格点上,请分别按不同要求在网格中描出一个格点
在格点上,请分别按不同要求在网格中描出一个格点![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
(1)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后所得的三角形,点
,画出旋转后所得的三角形,点![]() 旋转后落点为
旋转后落点为![]() .
.
(2)经过![]() ,
,![]() ,
,![]() 三点有一条抛物线,请找到点
三点有一条抛物线,请找到点![]() ,使点
,使点![]() 也落在这条抛物线上.
也落在这条抛物线上.
(3)经过![]() ,
,![]() ,
,![]() 三点有一个圆,请找到一个横坐标为2的点
三点有一个圆,请找到一个横坐标为2的点![]() ,使点
,使点![]() 也落在这个圆上.
也落在这个圆上.
(1)点![]() 的坐标为(
的坐标为(
(2)点![]() 的坐标为( , )
的坐标为( , )
(3)点![]() 的坐标为( , )
的坐标为( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着![]() 技术的发展,人们对各类
技术的发展,人们对各类![]() 产品的使用充满期待.某公司计划在某地区销售第一款
产品的使用充满期待.某公司计划在某地区销售第一款![]() 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第
产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第![]() (
(![]() 为正整数)个销售周期每台的销售价格为
为正整数)个销售周期每台的销售价格为![]() 元,
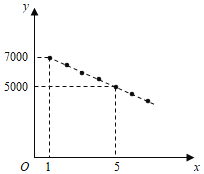
元,![]() 与
与![]() 之间满足如图所示的一次函数关系.
之间满足如图所示的一次函数关系.
(1)求![]() 与
与![]() 之间的关系式;
之间的关系式;
(2)设该产品在第![]() 个销售周期的销售数量为
个销售周期的销售数量为![]() (万台),
(万台),![]() 与
与![]() 的关系可用
的关系可用![]() 来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
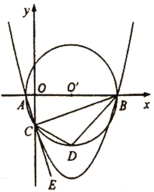
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 坐标为
坐标为![]() ,以
,以![]() 为直径作
为直径作![]() ,
,![]() 与抛物线交于
与抛物线交于![]() 轴上同一点
轴上同一点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)在(2)的条件下,抛物线上是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是BC边上的中点,连接AD.
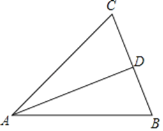
(1)在AB边上求作一点O,使得以O为圆心,OB长为半径的圆与AD相切;(不写作法,保留作图痕迹)
(2)设⊙O与AD相切于点M,已知BD=8,DM=4,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com